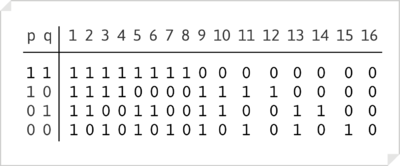(del griego λογική lógiké, derivado de logikós, que se refiere a la razón, de λόγος, logos, razón)
Ciencia formal que estudia las formas de los razonamientos bien hechos.
Es el procedimiento sistemático y fundado que nos permite diferenciar un razonamiento correcto, o válido de otro incorrecto, o inválido. Es, por lo mismo, estudio de la deducción lógica o de la inferencia lógica.
Puede también definirse como el estudio sobre la consistencia de los enunciados que afirmamos (ver cita), o como la ciencia de las reglas que nos permiten usar correctamente la expresión «por consiguiente», o un equivalente de la misma (ver cita).
Contenido
Argumentaciones
Los siguientes párrafos son ejemplos de argumentaciones o razonamientos
| 1. Siempre que se acerca la Navidad Ana está contenta;
estamos ya a 20 de diciembre; Por tanto Ana está contenta. |
| 2. Un caballo es un animal; por tanto, la cabeza
de un caballo es la cabeza de un animal (A de Morgan). |
| 3. Ninguna persona honesta roba; ahora bien, es
sabido que algunos personajes célebres roban; por tanto hay personajes célebres que no son honestos. |
| 4. Tengo ganas de descansar;
por consiguiente me voy de viaje. |
Puesto que son razonamientos válidos o correctos, los enunciados de que se compone cada uno de ellos son consistentes entre sí, el empleo de la expresión «por tanto» o equivalente es legítima, y, en cada caso, la conclusión ha sido deducida válidamente de las premisas.
Para que haya un razonamiento, no es preciso que la disposición de los enunciados sea la formal, la propia de la lógica; un razonamiento puede tener también una disposición informal, como en el ejemplo siguiente:
| Todos estamos locos por aquí. Yo estoy loco; tú
también lo estás [...] | |
| "¿Y cómo sabes tú si yo estoy loca?", le
preguntó Alicia. | |
| "Has de estarlo a la fuerza", le contestó el Gato;
"de lo contrario no habrías venido aquí". | |
| Alicia pensó que esto no probaba nada; pero continuó de
todas formas: "Y cómo sabes que tú estás loco?" | |
| "Para empezar," repuso el Gato, "los perros no están
locos, ¿de acuerdo?". | |
| "Supongo que no", repuso Alicia. | |
| "Bueno, pues entonces", continuó diciendo el Gato,
"verás que los perros gruñen cuando algo no les gusta, y mueven la cola cuando están contentos. | |
| En cambio yo gruño cuando estoy contento y muevo
la cola cuando me enojo. | |
| Luego, estoy loco" | |
| ______________________________________________ | |
| L. Carroll, Alicia en el país de las maravillas,
Alianza, Madrid 1983, p. 111. |
También aquí la conclusión se deduce correctamente -válidamente- de sus premisas. No es éste el caso, pese a las apariencias, del siguiente razonamiento:
- Si vas al polo norte has de abrigarte bien
- No vas al polo norte
- Luego no has de abrigarte bien
Razonamiento incorrecto ya que, el hecho de no ir al polo norte no significa que no se vaya a ir a otra zona fría donde sea necesario abrigarse.
La corrección -o validez- de un argumento no depende de que los enunciados de que se compone sean, de hecho, verdaderos o falsos, sino de si, entre premisas y conclusión, existe consecuencia lógica. La lógica estudia la consecuencia lógica desde un punto de vista formal, esto es, no atendiendo a la verdad de hecho de los enunciados, sino a la forma como se argumenta: si la forma de argumentar es correcta, entonces, si las premisas son verdaderas la conclusión será también verdadera. Hallar las formas correctas de argumentar supone hallar el criterio por el que decidimos que un razonamiento es válido o inválido.
Verdad y validez
Una cosa es que la conclusión sea verdadera y otra que su deducción sea válida. Una cosa es la verdad de las premisas y la conclusión, y otra la validez del razonamiento. Aquélla depende, según la teoría de la correspondencia, de si lo que el enunciado dice es, en realidad, lo mismo que sucede: ésta, de si la conclusión es una consecuencia lógica de las premisas. La validez depende de la forma como se argumenta y no del contenido de verdad o falsedad sus enunciados.
Un enunciado es consecuencia lógica de las premisas si es imposible que las premisas sean verdaderas y la conclusión falsa. Esto depende únicamente de la forma del razonamiento y no de ninguna verdad de hecho. Decimos, pues, que un razonamiento es válido -formalmente correcto- cuando su forma es tal que siempre que las premisas son verdaderas la conclusión también lo es, o bien cuando es imposible que las premisas sean verdaderas y la conclusión falsa. Y siempre y en todo caso, la validez de un razonamiento no depende de la verdad o falsedad de las premisas. Si el razonamiento es válido y, además, sus premisas son verdaderas, el razonamiento es también materialmente correcto, esto es, un razonamiento sólido.
En los razonamientos válidos, las premisas implican la conclusión. Y entonces, las premisas y la conclusión son necesariamente consistentes.
También puede decirse que un razonamiento es válido si su contraejemplo hace de las premisas y de la conclusión un conjunto de enunciados inconsistente.
En conclusión, sólo si razonamos correctamente, estamos legitimados a utilizar la expresión «por tanto», «por consiguiente» y otras equivalentes.
Lenguaje formal
Para estudiar la forma de los razonamientos, la lógica recurre a lenguajes formales. El mismo Aristóteles, fundador de la lógica, estudió la forma de los silogismos mediante esquemas de enunciados. Así, recurre a expresiones formales como: «Todo A es B», «B pertenece a todo A», o «B se predica de todo A». Con el desarrollo de la lógica moderna, llamada «lógica simbólica» o «lógica matemática» se han creado formalismos lógicos, lenguajes formales o cálculos lógicos.
Un lenguaje formal permite representar mediante fórmulas casi cualquier expresión de este mismo lenguaje, y amplía considerablemente la capacidad de formalizar -limitada a unos cuantos tipos de enunciados, preferentemente los categóricos- de la lógica clásica aristotélica, también llamada lógica tradicional.
Un lenguaje formal se identifica con el conjunto de fórmulas que pueden formarse siguiendo sus reglas: el conjunto de fórmulas bien formadas de un lenguaje.
Todo lenguaje formal supone:
- 1) un conjunto de símbolos, que constituyen el alfabeto del lenguaje, y
- 2) un conjunto de reglas de formación de fórmulas.
- Si se añade una tercera condición, a saber,
- 3) un conjunto de reglas de transformación de unas fórmulas en otras, se obtiene, además, un cálculo lógico o un procedimiento de deducción.
Un lenguaje formal o un cálculo lógico permite, en consecuencia, decidir:
- 1) si un símbolo pertenece al lenguaje;
- 2) si una fórmula determinada es una expresión bien formada del lenguaje; y
- 3) si una secuencia sintáctica de fórmulas constituye una demostración o una deducción.
En todo caso, un cálculo o un procedimiento de deducción pone de manifiesto que todo razonamiento válido equivale a una expresión lógica que siempre es verdadera. Una tal expresión es una «verdad lógica» o una «verdad formal».
La lógica de enunciados y la lógica de predicados son dos lenguajes lógicos formales. La distinción entre uno y otro se basa en la distinta capacidad expresiva del lenguaje. Los símbolos (alfabeto) del lenguaje de lógica de enunciados se refieren, básicamente, a enunciados y a conexiones entre enunciados, dejando intacta su estructura interna, mientras que los símbolos (alfabeto) de la lógica de predicados penetran en el interior de los enunciados y se refieren a los términos de que se componen los enunciados.
- 1.«Cuando sale el sol, amanece»
- es una expresión de lógica de enunciados, si de ella nos interesa la relación, o conexión, que se establece entre las dos oraciones simples, también llamadas atómicas:
- p = sale el sol
- q = amanece
- la relación «cuando» se simboliza mediante la conectiva «...si.... entonces» (formalmente [math](P\rightarrow{}Q)[/math]):
En cambio, el conjunto de enunciados
- 2. «Todo el que cree en la igualdad humana cree en la democracia
- Los estudiantes creen en la igualdad humana
- Luego los estudiantes creen en la democracia»
no quedaría suficientemente representado si escribiéramos:
- (p y q) luego r
Por esto, la lógica de predicados, analiza la estructura interna de estos enunciados, y permite escribir (según la lógica aristotélica):
- Todo A es B
- Todo C es A
- _________________
- Luego todo C es B
O bien según la lógica simbólica:
| [math]\forall{x}(Px \rightarrow{}Qx)[/math] |
| [math]\forall{x}(Rx \rightarrow{}Px)[/math] |
| ________________________________ |
| [math]\forall{x}(Rx \rightarrow{}Qx)[/math] |
El sistema de la lógica elemental, o de primer orden, se divide en lógica de enunciados y lógica de predicados.
Lógica de enunciados
Un enunciado es toda oración gramatical declarativa, esto es, aquella que es capaz de ser verdadera o falsa, dado que todo enunciado expresa -o significa- una proposición. El principio de bivalencia, uno de los fundamentos de la lógica clásica, establece además que todo enunciado, o proposición, ha de ser verdadero o falso, y no ambas cosas a la vez.
Los enunciados pueden ser simples (atómicos) o compuestos (moleculares) y se simbolizan mediante letras de enunciado (p, q, r, s,... minúsculas).
Los enunciados se combinan entre sí mediante conectivas lógicas, también llamadas operadores (porque operan entre enunciados). Los principales son: "no", "y", "o", "si..., entonces", "si y sólo si", y en símbolos
El lenguaje formal de la lógica de enunciados consta de:
1. Símbolos
- a) Letras de enunciado: p, q, r, s... (variables de enunciado)
- b) Operadores o conectores (o conectivas) [math]¬, \wedge, \vee, \to, \leftrightarrow[/math] (Constantes)
- c) Elementos auxiliares como (...), [...]
2. Reglas de formación de fórmulas
- a. Toda letra de enunciado es una fórmula bien formada (fbf) del lenguaje, y constituye un enunciado simple
- b. Si P es una fbf, también lo es ¬P
- c. Si [math]P[/math] y [math]Q[/math] son fbf, también lo son [math](P\wedge Q), (P\vee Q), (P\to Q), (P\leftrightarrow{Q})[/math]
- d. Ninguna otra expresión es una fórmula bien formada.
Los símbolos y las fórmulas constituyen la sintaxis del lenguaje formal y, con esta definición recursiva de fórmula, es posible decidir qué expresión pertenece a este lenguaje y expresar una cantidad indefinida de enunciados.
Ejemplo
No cualquier sucesión de símbolos es una fórmula bien formada, o una expresión del lenguaje. Así, por ejemplo,
no son fórmulas:
mientras que son fórmulas
[math]¬p\vee¬q [/math], por 2.b
[math] \neg (p \leftrightarrow q)[/math], por 2.aPero un lenguaje formalizado no consta sólo de una sintaxis (a saber, símbolos y reglas de formación de fórmulas), sino también de una semántica: ha de poder ser interpretado (ha de referirse a algo). Interpretar un lenguaje es atribuir significado a sus constantes (símbolos) y a sus variables (letras de enunciados). El significado que se le atribuye es el valor de verdad.
A todo enunciado descriptivo de carácter empírico, le asignamos un valor de verdad concreto -sabemos si es verdadero o falso- según su correspondencia con los hechos que describe; a un enunciado lógico, cuya referencia a los hechos se ignora metodológicamente, sólo podemos asignarle valores de verdad posibles:
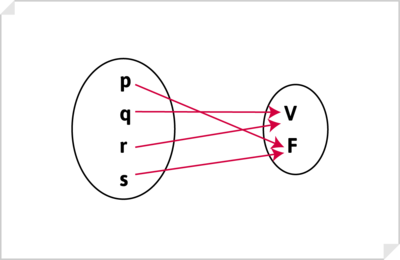
Así, a toda letra de enunciado se le asigna dos valores posibles: V y F (1, 0)
Una asignación de valores de verdad es una aplicación de un conjunto de letras de enunciado (argumento: p, q, r, s...) a un conjunto de valores de verdad (valor: V, F). Aplicamos a cada letra de enunciado un solo valor de verdad V (1) o de falsedad F (0).
En esta figura, a p se le asigna el valor F, a q el valor V, a r el valor V y a s el valor F.
Una asignación es una interpretación. Una interpretación es, por consiguiente, una aplicación o una función que asigna a una fórmula, o expresión de lógica de enunciados, sus posibles valores de verdad. El número de asignaciones para cada
Para una letra de enunciado,
p [math]=2^{1} [/math]
p = 1, p =0.
Para dos letras de enunciado,
p,q [math]=2^{2} [/math]
p = 1 y q = 1
p = 1 y q = 0
p = 0 y q = 1
p = 0 y q = 0
Para tres letras de enunciado,
p, q, r [math]=2^{3}[/math]
p = 1, q = 1 y r = 1
p = 1, q = 1 y r = 0
p = 1, q = 0 y r = 1
p = 1, q = 0 y r = 0
p = 0, q = 1 y r = 1
p = 0, q = 1 y r = 0
p = 0, q = 0 y r = 1
p = 0, q = 0 y r = 0
Para n letras de enunciado,
n [math]=2^{n}[/math]
A partir de la noción de asignación de valores es posible definir cada una de las conectivas como operadores veritativo-funcionales, porque, aplicadas a un enunciado simple (cuando se trata de ¬) o a dos enunciados simples (en los demás casos), dan un valor de verdad del enunciado compuesto que es función del valor de los enunciados que lo componen. Por esta razón las conectivas se definen de la siguiente manera:
Conectivas
«Una conectiva veritativo-funcional es una constante lógica que expresa una manera determinada de interpretar el valor de verdad de un enunciado compuesto a partir del valor de verdad de los componentes.»
La lógica define cada una de estas maneras mediante una [#tablasdeverdad tabla de verdad] propia de cada conectiva.
Puesto que no interesa el valor de verdad según el contenido material de los enunciados, se utilizan letras de enunciados (letras minúsculas; p, q, r,...) en lugar de enunciados (y para hablar de las letras de enunciados se utilizan también letras, esta vez, mayúsculas: P, Q, R,..., llamadas variables metalingüísticas).
Negación [math] \neg P[/math]
«No P es falso cuando P es verdadero y es verdadero cuando P es falso»
- Ejemplo
- Si es verdad que p («hace sol»), ¬p es falso («no hace sol» es falso)
- Si es falso que p (es falso que «hace sol»), ¬p es verdadero («no hace sol»)
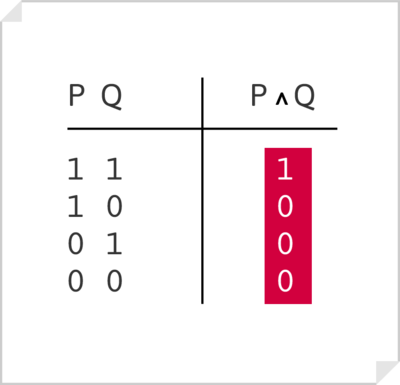
Conjunción [math]P\wedge Q[/math]
«P y Q ([math]P\wedge Q[/math])es verdadero sólo cuando sus enunciados componentes, P y Q son ambos verdaderos».
- Ejemplo
- Si p = "hace frío" y q = "hace viento", la fórmula [math]P\wedge Q[/math] ("hace frío y viento") es verdadera solamente si és verdad que "hace frío" y es verdad que "hace viento", en cualquir otro caso es falsa.
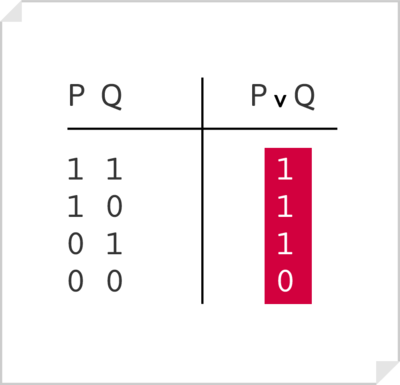
Disyunción [math]P\vee Q[/math]
«P o Q es verdadero cuando es verdadero P o cuando es verdadero Q, o lo son ambos a la vez».
- Ejemplo
- Si p = «Ana es buena» y q = «Ana parece buena», el enunciado «Ana es buena o lo parece» es verdad si resulta que es buena o si sólo lo parece, o si es buena y, además, lo parece.
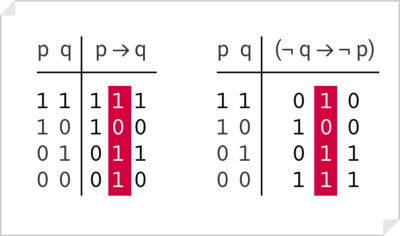
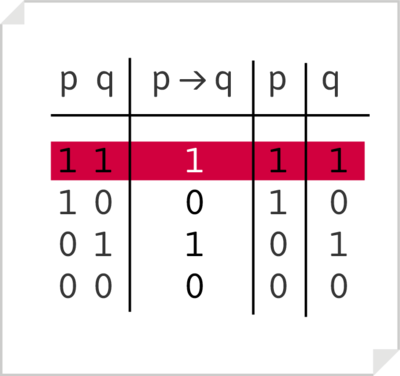
Condicional [math]P\rightarrow{}Q[/math]
«Si P, entonces Q es verdadero siempre, menos cuando el antecedente, P, sea verdadero y el consecuente, Q, falso».
- Ejemplo:
- Si alguien dice: p = "Ana estudia, q = "Ana aprueba", la fórmula [math]p\rightarrow{}q[/math], que lee "si Ana estudia, aprueba" (o "Si Ana estudis, entoces aprueba")es verdadera en los casos siguientes:
- Ana estudia y aprueba
- Ana no estudia pero aprueba
- Ana ni estudia ni aprueba
- Solamente es falso el enunciado si Ana estudia pero no aprueba.
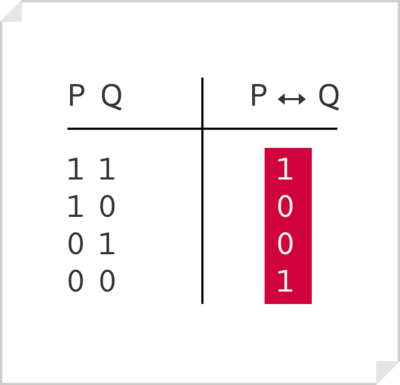
Bicondiconal [math]P \leftrightarrow Q[/math]
«P si y sólo si Q es verdadero cuando P y Q son ambos verdaderos o ambos falsos; en los demás casos, es falso».
- Ejemplo
- Si p = eres feliz» y q = «amas», el enunciado «eres feliz si y sólo si amas», o «eres feliz siempre y cuando ames» es verdad cuando «eres feliz y amas» y cuando «ni eres feliz ni amas», pero es falso si es verdad una de ambas cosas y no la otra.
Otras conectivas posibles
El número de funciones de verdad posibles (N) responde a la fórmula combinatoria
[math]N=m^{^{m^{n}}}[/math]
donde n es el número de letras de enunciado y m los valores de verdad (V y F) y m, como número base, las dos combinaciones posibles del valor global de V y F para cada asignación. Para una expresión lógica de dos letras de enunciado,
[math]N=2^{^{2^{2}}}[/math]
por lo que, para dos enunciados, p y q, las funciones de verdad posibles son, por tanto, 16. Cada una de las columnas de la siguiente tabla son sus definiciones.
Cada una de estas columnas describe una posible función de verdad, según la fórmula mencionada; las columnas 9-16 son la negación de su simétrica en las columnas 8-1, por este orden. Las columnas 2, 5, 7, y 8 son las usuales funciones de verdad definidas (disyunción, condicional, bicondicional y conjunción), y la 11 y la 13, la negación (de q y de p, respectivamente).
| columna 1: tautología
[math](p\vee ¬p)\wedge (q \vee ¬q)[/math] |
columna 2: disyunción inclusiva
[math](p\vee q)[/math] |
| columna 3: condicional material inversa
[math](q\rightarrow p)[/math] |
columna 4: afirmación de p
[math](p)[/math] |
| columna 5: condicional material
[math](p\rightarrow q)[/math] |
columna 6: afirmación de q
[math](q)[/math] |
| columna 7: bicondicional
[math](p\leftrightarrow q)[/math] |
columna 8: conjunción
[math](p\wedge q)[/math] |
| columna 9: incompatibilidad (p/q) Barra o functor de Scheffer
[math](¬p\vee ¬q), ¬(p\wedge q), o (p\rightarrow ¬q)[/math] |
columna 10: disyunción exclusiva
[math]p\veebar q[/math] |
| columna 11: negación de q
[math](¬q)[/math] |
columna 12: afirmación de q y negación de p
[math]¬(q\rightarrow p)= (q\wedge ¬p)[/math] |
| columna 13: negación de p
[math](¬p)[/math] |
columna 14: afirmación de q y afirmación de p
[math]¬(p\rightarrow q)= (p\wedge ¬q)[/math] |
| columna 15: [math](p\downarrow q)[/math] negación de la disyunción, o functor de Peirce
[math]¬(p\vee q), (¬p\wedge ¬q)[/math] "solamente es verdadera si ambos enunciados son falsos" |
columna 16: contradicción
[math](p\wedge ¬p)\vee (q\wedge ¬q)[/math] |
Nota: Las funciones expresadas en las columnas 9 y 15 (functor de Sheffer y functor de Peirce, respectivamente) se consideran conectivas adecuadas: ellas solas pueden representar todas las restantes.
(Repetimos la misma tabla de valores para poder visualizar adecuadamente la explicación de cada columna)
Tablas de verdad
Algoritmo que permite demostrar si una expresión de lógica de enunciados es o no una fórmula lógicamente verdadera.
La noción de función de verdad, que permite crear tablas de todos los posibles valores de verdad de una fórmula, permite también analizar el de cualquier expresión de lógica de enunciados. Por ello, una tabla de verdad es también un método o procedimiento semántico que:
- 1) Permite decidir si una fórmula es una tautología, una contradicción, o una expresión consistente, y si dos o más fórmulas son lógicamente equivalentes. Y en conexión con esto, en el supuesto de que todo razonamiento formalmente válido es una tautología -una implicación siempre verdadera-
- 2) permite decidir si una secuencia de enunciados, o de fórmulas de lógica de enunciados, constituye un razonamiento válido.
Fórmulas tautológicas
Una fórmula es una tautología si es verdadera para cualquier asignación de valores de verdad. En una tabla de verdad, la tautología da siempre valores verdaderos.
- Ejemplo
Fórmulas contradictorias
Una fórmula es contradictoria si es falsa para cualquier asignación de valores de verdad.
- Ejemplo
Fórmulas consistentes
Una fórmula es consistente si hay por lo menos una asignación que la hace verdadera; si no es, por tanto, ni tautológica ni contradictoria.
- Ejemplo
Fórmulas equivalentes
Dos fórmulas son equivalentes si las asignaciones de valores que hacen verdadera a una de ellas hacen también verdadera a la otra, y viceversa, y si las asignaciones de valores que hacen falsa a una de ellas hacen también falsa a la otra, y viceversa.
Las tablas de dos fórmulas equivalentes son iguales.
- Ejemplo
Las tablas permiten, además, comprobar la consecuencia lógicay permiten también comprobar la independencia lógica entre enunciados o fórmulas
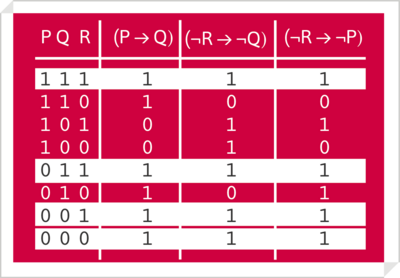
- Ejemplo de comprobación de consecuencia lógica
- Sea [math](P\rightarrow{}Q), (¬R\rightarrow{}¬Q), \models (¬R\rightarrow{}¬P)?[/math]
- la tabla de verdad prueba que [math](¬R\rightarrow{}¬P)[/math]
- es una consecuenia lógica del comjunto [math]\Delta[/math] de fórmulas
- [math][(P\rightarrow{}Q), (¬R\rightarrow{}¬Q)[/math]
- puesto que toda interpretación que hace verdader al conjunto [math]\Delta[/math] hace también verdadera la fórmula [math](¬R\rightarrow{}¬P)[/math]
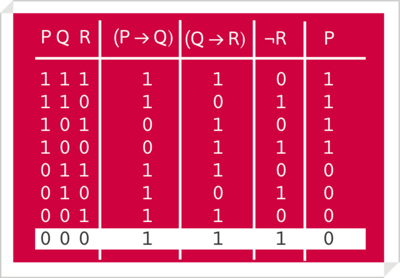
- Ejemplo de comprobación de independencia lógica entre enunciados o fórmulas
- Sean los enunciados [math](P\rightarrow{}Q), (Q\rightarrow{}R), ¬R, \models P?[/math].
- La tabla de verdad prueba que el enunciado P es independiente del resto de enunciados.
Razonamientos válidos
Con las nociones introducidas hasta aquí, se dispone ya de un lenguaje formalizado, con el que es posible expresar cualquier razonamiento de lógica de enunciados; basta indicar los métodos que deciden cuáles son las secuencias de fórmulas que representan un razonamiento válido. Sobre estas secuencias de fórmulas, es posible hacer afirmaciones de tipo semántico, basadas en la atribución de la noción de verdad, o bien de tipo sintáctico, basadas en la noción de equivalencia. Las primeras son propias de los métodos semánticos, y las segundas de los sintácticos.
Métodos semánticos
1) Un razonamiento es válido si, siempre que sus premisas son verdaderas, la conclusión también es verdadera, y no es posible que, con premisas verdaderas, la conclusión pueda ser falsa.
2) Un razonamiento válido es, en consecuencia, una implicación formalmente válida. Por lo mismo, un razonamiento es válido, si el secuente semántico que forman sus premisas y su conclusión constituye una tautología.
Un secuente es una afirmación (hecha en metalenguaje) sobre un conjunto de fórmulas lógicas (las premisas y la conclusión), utilizando el signo de «consecuencia lógica». Por ejemplo, el conjunto [math](p\rightarrow{}q), p \models q[/math], donde el signo [math]\models[/math] significa "consecuencia lógica", puede representar a modo de esquema el razonamiento siguiente:
- «Si Ana sueña, duerme
- Ana está soñando,
- por tanto duerme»
del que se afirma que si los dos primeros enunciados son verdaderos, lo es también el tercero: que éste se sigue lógicamente de los otros dos..
Uso de tablas
Dos son las maneras como podemos utilizar las tablas para demostrar la validez de un razonamiento.
Consecuencia lógica
Una fórmula, llamada conclusión, es una consecuencia lógica de otra u otras, llamadas premisas, si toda interpretación -o asignación de valores de verdad- que hace verdaderas a las premisas hace también verdadera a la conclusión:
Para la asignación de valores de la primera línea, se cumple que «la interpretación que hace verdadero al conjunto de premisas hace también verdadera a la conclusión».
Por tanto, q es consecuencia lógica del conjunto dado de fórmulas, como expresa el secuente semántico: [math](p\rightarrow{}q), p \models q[/math]
Implicación tautológica:
En el supuesto de que sea un razonamiento válido, el ejemplo mencionado puede escribirse como una implicación : [math][(p\rightarrow{}q)\wedge p]\rightarrow{}q[/math]
La tabla de verdad muestra que este condicional es una tautología.
Es una implicación verdadera en todo caso, por lo que se cumple que «siempre que las premisas son verdaderas la conclusión también lo es, y en ningún caso sucede que las premisas sean verdaderas y la conclusión falsa».
Por consiguiente, tanto por (1) como por (2), se muestra que el razonamiento es válido.
En resumen, en un razonamiento válido hay consecuencia lógica entre premisas y conclusión: [math]A_1, A_2, ... A_n \models B[/math]
O bien, si B es válido sin premisas: [math]\emptyset\models B[/math]
Lo cual significa simplemente que B es una tautología, o una fórmula universalmente válida (ver lista de tautologías).
Árboles lógicos
Este método llamado también cálculo de los árboles lógicos iniciado por E.W. Beth (1955), es un método semántico que permite verificar si una fórmula es una tautología o si una fórmula es una consecuencia lógica de sus premisas, recurriendo al concepto de consistencia.
Permite demostrar tanto que [math]\emptyset\models B[/math], como que [math]A_1, A_2, ... A_n \models B[/math]
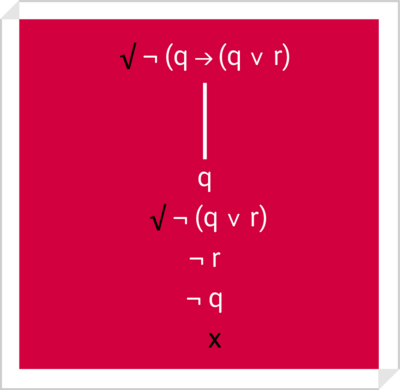
Se demuestra que [math]\models ¬B[/math] es una contradicción (Ejemplo 1)
- Sea la tautología [math]q\rightarrow{}(q\vee r)[/math]. Su árbol lógico es:
- Por consiguiente si [math]¬q\rightarrow{}(q\vee r)[/math] es una contradicción, [math]q\rightarrow{}(q\vee r)[/math] és una tautología.
, o que el conjunto constituido por las premisas y la negación de la conclusión, que constituye su contraejemplo, [math]A_1, A_2, ... A_n \models ¬B[/math] es inconsistente
Ver
- Ejemplo 2
y
- Ejemplo 3
- Sea el razonamiento siguiente: "Cuando Ana canta, la acompaña Raúl o lo hace Sabino. Pero hoy no la acompaña Raúl, por tanto, puesto que Sabino tampoco la acompaña, Ana no canta".
- Que puede formalizarse de la siguiente manera: [math][(p\rightarrow{}(q\vee r))\wedge ¬q]\rightarrow{}(¬r\rightarrow{}¬q)[/math].
- Su árbol lógico es:
-
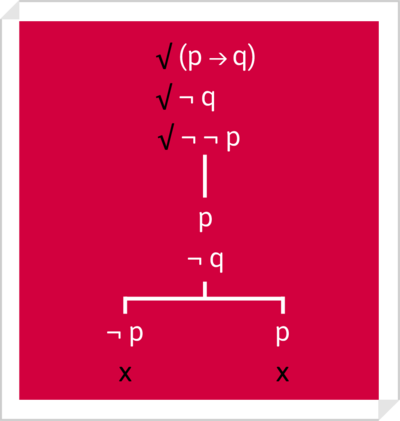
- El conjunto formado por las premisas dadas y la negación de la conclusión (el contraejemplo) es inconsistente; por tanto el razonamiento es válido.
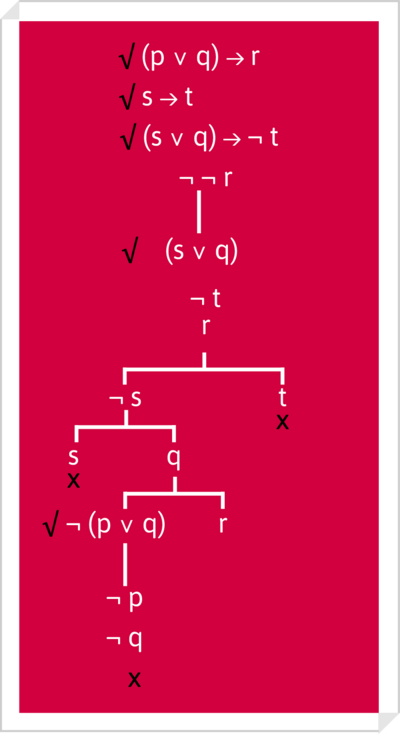
- En cambio en el siguiente caso, el razonamiento no es válido.
- Sea [math]((p\vee q)\rightarrow{}r), s\rightarrow{}t, ((s\vee q)\wedge ¬t), \vdash ¬r?[/math]. Su árbol lógico es:
- La rama en que se halla [math]r[/math] no está cerrada; por tanto, el conjunto formado por las premisas y la negación de la conclusión no es inconsistente. Por consiguiente el conjunto dado [math]((p\vee q)\rightarrow{}r), s\rightarrow{}t, ((s\vee q)\wedge ¬t, \vdash ¬r?[/math] es inconsistente, y la rama que queda sin cerrar incluye los valores del contraejemplo.
- Basta una sola combinación de valores que hagan inconsistente el conjunto para que dispongamos de un contraejemplo que hace inválido el razonamiento. (En este caso, p=0 o 1, q=1, r=1, s=0, t=0).
Véase la descripción del método en cálculo de los árboles lógicos.
La noción lógica fundamental en los métodos de tablas es la de no contradicción o consistencia entre premisas y conclusión. En los métodos sintácticos la noción lógica fundamental es la de equivalencia entre fórmulas que preservan, o transmiten, la verdad.
Métodos sintácticos
Los métodos sintácticos consisten en derivar o deducir una conclusión, a partir de unos principios o unas premisas dadas. Un razonamiento es, así, válido si la conclusión se ha derivado o deducido correctamente de sus principios o premisas mediante reglas; la validez se entiende ahora como deducibilidad. En los métodos semánticos, razonamiento válido es aquel que no admite la posibilidad de que sus premisas sean verdaderas y la conclusión falsa; en los métodos sintácticos es aquel cuya conclusión se ha demostrado, derivado o deducido correctamente de principios o premisas (hipótesis). Lo cual se expresa mediante el siguiente secuente sintáctico: [math]A_1,A_2,...A_n \vdash B[/math] que se lee "B es demostraba a partir de principios o premisas", o "B es deducible", y donde el signo [math]\vdash[/math] representa la deducibilidad de de la fórmula B respecto de otra u otras. Si el conjunto de premisas es el conjunto vacío, entonces [math]\emptyset\vdash B[/math], o bien [math]\vdash B[/math], y, en este caso, B es un teorema de la lógica. El teorema de la deducción (Herbrand, 1930) establece que si [math]A_1, A_2, ... A_n \vdash B[/math], entonces [math]\models A_1, A_2, ...A_n \rightarrow{} B[/math], de modo que, si B se deduce formalmente a partir de un conjunto de premisas, entonces la implicación que forman estas premisas y la conclusión B constituyen una fórmula universalmente válida.
a) Métodos axiomáticos
El método más clásico de deducción lógica. Un sistema formal axiomático se compone de una lista de axiomas y de una o más reglas de inferencia.
Cualquier fórmula (B) de esta secuencia es un teorema sintáctico [math]\vdash B[/math] si se demuestra a partir de los axiomas. Una demostración o derivación axiomática de B es:
- 1) una secuencia finita de fórmulas
- 2) cuya última fórmula es B;
- 3) donde cada fórmula es o un axioma o una consecuencia de un axioma derivada mediante reglas de inferencia.
A los sistemas axiomáticos, cuya característica general es, por un lado, la simplicidad -tienen, por lo común, pocas reglas de inferencia- y, por el otro, la laboriosidad de las demostraciones (ver ejemplo) siguen, como alternativa, a partir de 1934, los sistemas de deducción natural,ideados por G. Gentzen.
b) Deducción natural
Uno de los sistemas formales de deducción, empleados en lógica, ideado independientemente por Gerhard Gentzen (1909-1945), lógico y matemático alemán discípulo de Hilbert, y Stanislaw Jaskowsky, en 1934. Consiste en un procedimiento de derivación para probar la validez de una conclusión, partiendo de premisas iniciales y deduciendo nuevas premisas intermedias mediante reglas de inferencia, cuyo uso se justifica. No recurre a axiomas y el procedimiento demostrativo en conjunto tiene cierta semejanza con la manera «natural» de deducir.
Utiliza reglas de inferencia para cada una de las conectivas y, como presupuesto fundamental, admite suponer como premisa cualquier enunciado, que puede introducirse condicionadamente en cualquier momento de la demostración (suposición que eventualmente debe cancelarse recurriendo a la demostración condicional o a la prueba por reducción al absurdo;
- Ejemplo:
- Puede demostrarse, por ejemplo, que la fórmula [math](P\wedge Q)\rightarrow{}Q[/math] es un teorema de la lógica de enunciados, que puede ser deducido sin recurrir a premisas:
- 1. [math]P\wedge Q[/math] suposición
- 2. [math]Q[/math] por eliminación del conjuntor en 1
- 3. [math](P\wedge Q)\rightarrow{}Q[/math] prueba del condicional en 1 y 2
- O también que [math](P\rightarrow{}R)[/math] es una consecuencia lógica de [math](P\rightarrow{}Q)[/math] y [math](Q\rightarrow{}R)[/math] razonando de la siguiente manera:
- 1. [math]P\rightarrow{}Q[/math]
- 2. [math]Q\rightarrow{}R[/math]
- 3. [math]P[/math] suposición
- 4. [math]Q[/math] MP 1,3
- 5. [math]R[/math] MP 2,4
- 6. [math]P\rightarrow{}R[/math] IC 3-5
- razonamiento que es la justificación del «silogismo hipotético».
Como ejemplo de sistema de deducción natural utilizamos las ocho reglas básicas de Gentzen y algunas de las derivadas (Ver, por ejemplo, M. Garrido, Lógica simbólica, Tecnos, Madrid 1983, p. 84 y p. 96-99.).
Usando dichas reglas Si se quiere probar la validez del siguiente razonamiento: [math][(r\rightarrow{¬s})\wedge(p\rightarrow{r})\wedge p]\rightarrow{(¬s\vee t)}[/math]
aplicando las reglas básicas del cálculo de lógica de enunciados,
se demuestra que [math](¬s\vee t)[/math] es deducible del conjunto de premisas [math](r\rightarrow{}¬s), (p\rightarrow{}r), p[/math]
Si se quiere probar la validez que [math](p\rightarrow{¬s})[/math] es deducible del conjunto de fórmulas [math](p\wedge s)\rightarrow{q}, (q\rightarrow{t}), (¬t\wedge s)[/math], esto es, [math](p\wedge s)\rightarrow{q}, (q\rightarrow{t}), (¬t\wedge s) \vdash (p\rightarrow{¬s})[/math], aplicando reglas básicas y derivadas, se obtiene:
Con ello se demuestra que [math][(p\wedge s)\rightarrow{q} \wedge (q\rightarrow{t}) \wedge (¬t\wedge s)]\rightarrow{}(p\rightarrow{¬s})[/math]
Conclusión
La lógica de enunciados es un sistema formal que posee unos procedimientos de decisión efectivos para probar que una fórmula cualquiera es también una consecuencia lógica. Por consiguiente constituye un sistema formal decidible, ya que estos procedimientos son eficaces para decidir, semánticamente, si una fórmula es una tautología o si es, sintácticamente, un teorema del cálculo (sistema axiomático.
Como sistema formal, la lógica de enunciados posee también las propiedades de consistencia y completud. Posee la propiedad de consistencia, dado que para cualquier fórmula válida, A, de lógica de enunciados, es verdad que
Lo cual afirma su consistencia interna y excluye que sea posible demostrar A y ¬A, contradictorias entre sí. O lo que es lo mismo, afirma que todos sus teoremas son válidos.
Es, además, un sistema formal completo, dado que cualquier forma válida puede ser demostrada dentro de la lógica de enunciados. Y, así, para cualquier fórmula, A, es verdad que
Ésta es la propiedad recíproca, o conversa, de la anterior, de modo que, al afirmarse ambas, las dos propiedades anteriores dan lugar a la siguiente equivalencia
El significado de esta equivalencia es doble:
1) Todas las secuencias que son deducciones formales son también formalmente verdaderas y, a la inversa, todas las secuencias formalmente verdaderas son susceptibles de una demostración formal; y
2) toda deducción es una verdad lógica y todas las verdades lógicas son demostrables; o todo teorema es una tautología, y toda tautología es un teorema del sistema.
La lógica de enunciados es, por tanto, un sistema formal consistente, completo y decidible.
Lógica de predicados
Parte de la lógica que tiene como objeto de estudio la consecuencia lógica entre enunciados, cuando para decidirla no basta considerar la estructura global de los enunciados, sino que es necesario conocer su estructura interna. Es, en consecuencia, el estudio de las inferencias válidas que se basan en la estructura interna de los enunciados. David Hilbert y Wilhelm Ackermann fueron los primeros en describir de un modo sistemático (1928) esta parte de la lógica, propiamente llamada lógica de predicados de primer orden.
La lógica de enunciados no puede analizar satisfactoriamente razonamientos como los dos siguientes:
1- Todos los que cantan son personas sensibles
Raúl canta |
| Por tanto Raúl es una persona sensible |
2) Todas las personas sensibles cantan
Raúl canta |
| Por tanto, Raúl es una persona sensible |
En lógica de enunciados estos dos razonamientos (valido el primero, inválido el segundo) tendrían el mismo esquema de argumento: si [math]A_1[/math] y [math]A_2[/math], entonces [math]B[/math], lo cual no permite decidir cuál de los dos es válido.
La lógica de predicados, al analizar la estructura interna de la frase y al introducir operadores internos, permite diferenciar entre objetos o individuos, propiedades y relaciones.
En «Todo hombre razona», podemos diferenciar el objeto o individuo (el sujeto gramatical) del que se habla, y que aquí se precisa que se trata de «todos los hombres», y la propiedad que atribuimos a este objeto o individuo, que aquí es el predicado «_______ razona». Hay predicados que se refieren a más de un objeto (como, por ejemplo, en «_______es el padre de_______» o «_______ está entre_______ y _______», que son relaciones).
Una cosa es ser «objeto» o «referente» y otra distinta ser «predicado»; los términos que designan objetos son designadores, y los que designan predicados, relatores. Asimismo, al objeto o referente que puede ocupar el espacio vacío « _______ ... » se le llama argumento; a un argumento se le atribuyen predicados, que son propiedades (predicados absolutos)o relaciones (predicados relativos). Inversamente, a las propiedades corresponden argumentos que son nombres, pronombres u objetos y, a las relaciones, parejas de nombres, o más, según sean los predicados diádicos, triádicos, n-ádicos (o binarios, ternarios, n-arios, etc.), esto es, según los predicados tengan dos o más lugares vacíos.
El lenguaje de la lógica de predicados
La lógica de predicados es un lenguaje formal cuyos enunciados son fórmulas con las que simboliza y analiza la estructura interna de las frases. Este lenguaje artificial está formado por símbolos y fórmulas:
- Símbolos
- Fórmulas
Ejemplos :
1. Enunciados cuantificados.
- Ejemplo
| Enunciado |
| lenguaje lógico |
| lenguaje ordinario |
| [math] \forall{x} (Rx)[/math] |
| Para cualquier x, x es rojo |
| Todo es rojo |
| [math] \forall{x} (Rx→Ex)[/math] |
| Para cualquier x, si x es rojo, x es extenso |
| Todo lo rojo es extenso |
| [math] \forall{x} (Rx\leftrightarrow{Ex})[/math] |
| Para cualquier x, x es rojo si y sólo si x es extenso |
| Todo es rojo y extenso o ni rojo ni extenso |
| [math] ¬\forall{x} (Rx)[/math] |
| No es el caso que, para todo x, x sea rojo |
| No todo es rojo |
| [math]\forall{x} (¬Rx)[/math] |
| Para todo x, x no es rojo |
| Nada es rojo |
| [math]( ¬\forall{x} (Rx→Ex))[/math] |
| No es el caso que, para todo x, si x es rojo entonces x es extenso |
| No todo lo que es rojo es extenso |
| [math](\forall{x} (Rx→¬Ex))[/math] |
| Para todo x, si x es rojo, entonces x no es extenso |
| Nada rojo es extenso |
| [math]\exists{x}(Rx)[/math] |
| Existe algún x tal que x es rojo |
| Algo es rojo |
| [math]\exists{x}(Rx \wedge Ex)[/math] |
| Hay algún x tal que x es rojo y extenso |
| Algo es rojo y extenso a la vez |
| [math]¬(\exists{x}(Rx))[/math] |
| No es el caso que exista un x tal que x sea rojo |
| Nada es rojo |
2. Enunciados cuantificados con más de una variable
- Ejemplo
[math] \forall{x} \forall{y} (Axy\rightarrow{Gxy})[/math]
Para todo x y para todo y, si x ama a y, y se siente agradecida a x;
Siempre que una persona ama a otra ésta se lo agradece.
[math] \forall{y} \exists{x}(Gxy)[/math]
Para todo y hay algún x que es su alma gemela;
Toda alma tiene su alma gemela.
[math] \forall{y} \exists{x}(Axy)[/math]
Para todo y hay algún x que ama a y;
Todo el mundo ama a alguien.
[math] \forall{x} \forall{y} (Axy)[/math]
Para todo x y para todo y, x ama a y;
Todo el mundo ama a todo el mundo.
[math]\exists{x} \exists{y} (Axy)[/math]
Para algún x y para algún y, x ama a y;
Alguien ama a alguien.
[math]\exists{x} \forall{y} (Axy)[/math]
Para algún x y para todo y, x ama a y;
Alguien ama a todo el mundo.
[math] \forall{x} \forall{y} (¬Axy \longrightarrow{Mxy})[/math]
Para todo x y para todo y, si no sucede que x es amigo de y, x se siente molesto con y;
Cuando no se es amigo de alguien nos es fácil sentirnos molestos con él.
[math]¬ \forall{x} \forall{y} (Axy)[/math]
No para todo x y para todo y, x ama a y;
No todo el mundo ama a todo el mundo.
También la lógica de predicados goza de las propiedades de consistencia y completud (en sentido débil: cuando toda fórmula válida es también un teorema), de modo que todo enunciado o fórmula deducible es una verdad lógica, y toda verdad lógica es deducible o derivable; pero la lógica de predicados, globalmente considerada, no es decidible. A diferencia de la lógica de enunciados, no dispone de un procedimiento mecánico, de un algoritmo universal, como son las [#tablasdeverdad tablas de verdad], para decidir si una fórmula cualquiera es universalmente válida
Ejemplo
De un enunciado como [math] \forall{x} Px[/math] puede deducirse [math]\exists{x} Px[/math], y esta deducción puede hacerse sin premisas. Por consiguiente, es posible escribir [math]\vdash \forall{x} Px \rightarrow{\exists{x} Px}[/math] y, por lo mismo, suponer que [math]\models \forall{x} Px \rightarrow{\exists{x} Px}[/math]
Pero esta última fórmula, aunque necesariamente verdadera, no es una tautología. Su verdad se demuestra sólo como conclusión de una demostración o derivación.
La única manera de probar, para partes determinadas de esta lógica, que una fórmula es universalmente válida, o que un argumento es válido, es por medio de una deducción. Entonces se cumple que [math]A_1, A_2, ... A_n \vdash B[/math], y si [math]\vdash B[/math], entonces [math]\models B[/math]
Y esto prueba la consistencia de la lógica de predicados: todo lo que es deducible es lógicamente verdadero, o que sólo las fórmulas universalmente válidas son teoremas. Y de ahí, la importancia de los métodos deductivos, o cálculos, en lógica de predicados
Sistemas formales de deducción
Aparte de los sistemas axiomáticos, los sistemas deductivos más utilizados son los árboles lógicos (el mismo, sustancialmente, que en el cálculo de enunciados) y la deducción natural.
Árboles lógicos
Permiten decidir la validez de algunas argumentaciones de lógica de predicados, dado que, si bien no pueden demostrar la consistencia de todas las fórmulas con cuantificadores, pueden demostrar la inconsistencia.
Sus reglas son las mismas del cálculo de enunciados más cuatro propias de los cuantificadores (ver reglas).
Ver ejemplos:
Ejemplo.
Supongamos el ejemplo siguiente:
La crítica que procede de una cierta necesidad psicológica de hacerla en aquellos que la hacen no merece una respuesta racional. Cuando la gente se queja de que el psicoanálisis sostiene afirmaciones bárbaras y arbitrarias sobre la sexualidad infantil, su crítica procede de determinadas exigencias psicológicas de esta misma gente. Por consiguiente la crítica que se basa en decir que el psicoanálisis sostiene afirmaciones bárbaras y arbitrarias sobre la sexualidad infantil no merece una respuesta racional.
(Texto arreglado, procedente de la Conferencia XXXIV de Nuevas aportaciones al psicoanálisis, en S. Freud, Obras completas, 3 vols., Biblioteca Nueva, Madrid 1968, vol. II, p. 943-953).
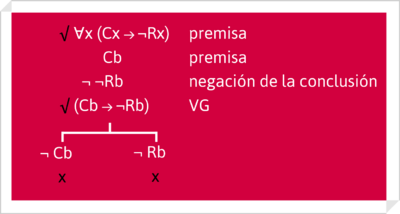
Sea la siguiente interpretación:
Cx: x es una crítica que procede de una cierta necesidad psicológica de hacerla en aquellos que la hacen.
Rx: x merece una respuesta racional.
b: la queja de que el psicoanálisis sostiene afirmaciones bárbaras y arbitrarias sobre la sexualidad infantil.
Transcritas como fórmulas, tenemos el siguiente razonamiento:
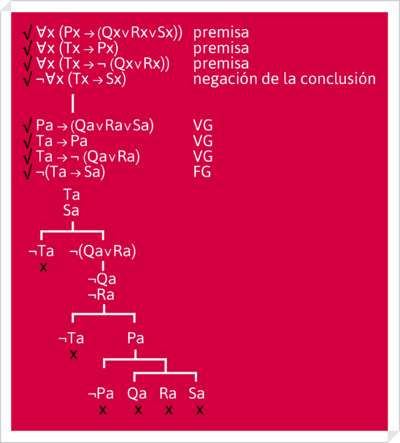
[math][ \forall{x} (Cx\rightarrow{¬Rx})\wedge Cb]\rightarrow{¬Rb}[/math]
Su prueba mediante un árbol muy breve. Sólo utiliza una regla (la VG):
Ejemplo tomado de W. Hodges, Logic, Penguin Books, Londres 1991, p.230-231
Ejemplo.
Todo lo que agrada es ilegal, o inmoral o engorda. Tomarse un helado es agradable. Tomarse un helado no es ilegal ni inmoral. Por tanto, tomarse un helado engorda.
Su formalización es:
Deducción natural
Utiliza las mismas reglas del cálculo de lógica de enunciados más cuatro reglas básicas propias del cálculo de predicados, y algunas derivadas (ver reglas).
Ejemplos :
Lógica de clases
La lógica que trata de las clases y de los miembros de las clases. Se identifica con la lógica de predicados monádicos, y en ella se distinguen dos partes: el álgebra de clases y la lógica de clases propiamente dicha.
El álgebra de clases puede considerarse como una interpretación extensional de la lógica de enunciados, donde las letras no significan enunciados, sino clases, esto es, el conjunto de objetos o individuos que tienen la misma propiedad: una clase es la extensión de un predicado. La expresión «x es pianista» se interpreta como «x es miembro de la clase de pianistas» = Px. Todo objeto que tenga la propiedad de «ser pianista» pertenece a esta clase. La clase de todos estos objetos con esta propiedad se escribe con el operador de abstracción
[math]P=_{df}[/math]{[math]{\hat{x} Px}[/math]} y se lee "la clase de todos los x tales que x es P".
Se distingue entre clases finitas (por ejemplo, los días de la semana) e infinitas (por ejemplo, la serie de números naturales); clases unitarias, con un único elemento (por ejemplo, el número B); clase vacía, (por ejemplo, una semana de sólo tres días) y clase universal o universo de discurso, representada por la clase donde cobra sentido hablar de otras clases y sus propiedades; hablar de «atletas» y de sus «marcas» tiene sentido en un universo de hombres y mujeres.
Se distinguen, asimismo, operaciones entre clases y relaciones entre clases. El resultado de estas últimas son enunciados sobre clases; el resultado de las primeras es una nueva clase.
Operaciones entre clases:
Son las clases producidas por los operadores de clase «productor», «sumador» y «complementador»
[math]\cap, \cup, \bar{} [/math]
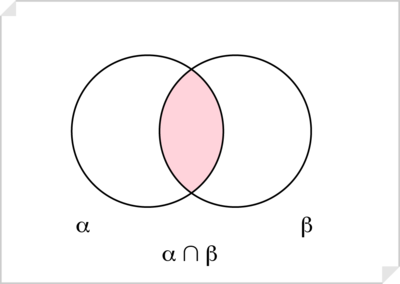
La intersección , multiplicación lógica, o clase producto, [math]A\cap B[/math] está formada por los individuos que pertenecen, a la vez, a A y a B. Así, «filósofos españoles» es la intersección entre la clase de «filósofos» y la de «españoles».
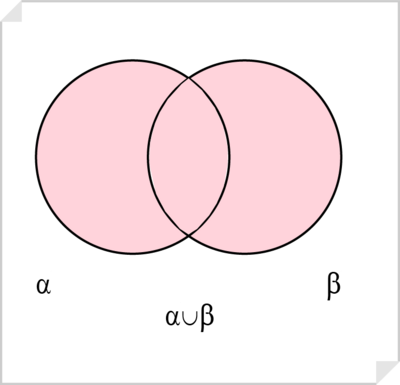
La unión , o suma lógica, o clase suma, [math]A\cup B[/math] es la clase formada por los individuos que pertenecen a una de las dos clases o a ambas. La clase del «personal sanitario» está constituida por médicos, personal A.T.S. y por aquellos -si los hay- que son ambas cosas a la vez.
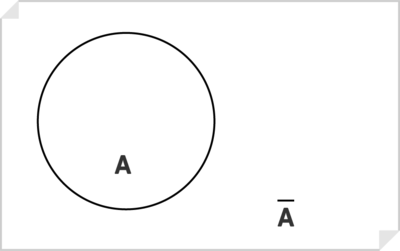
La clase complemento o complementaria de [math]A \overline{A}[/math] es aquella a la que pertenecen los elementos que no pertenecen a A: la clase complemento de los días festivos de un mes son todos los demás días laborables.
Clases disyuntas son aquellas cuya intersección es vacía. La clase de los «hombres» es disyunta de la de los «animales que vuelan», porque «Ningún hombre vuela». Por ello, los enunciados categóricos de forma E pueden escribirse como
[math]A\cap B = 0[/math]
De la misma manera que los enunciados categóricos de forma A pueden escribirse como una clase disyunta de una clase A y la clase complemento de otra
[math]A\cap \overline{B} = 0[/math]
En cambio, los enunciados categóricos particulares afirman que dos clases no son disyuntas, una respecto de otra. Así, «algunos mamíferos viven en el mar», enunciado de tipo I, puede escribirse como
[math]A\cap B \neq 0[/math]
que afirma que la intersección de A y B no es vacía. Por lo mismo, un enunciado de tipo O, como «algunas expresiones no son afortunadas», se escribe como una intersección no vacía entre una clase, A, y la clase complemento de B
[math]A\cap \overline{B} \neq 0[/math]
Relaciones entre clases
Enunciados sobre clases, construidos con las constantes de enunciados de clase [math]"\subset, = "[/math]
La inclusión de clases, que se escribe
[math]A\subset B[/math]
se lee como «A está contenida en B» y se define afirmando que si algo pertenece a A, pertenece también a B, por lo que A es una subclase de B. El enunciado «los españoles son europeos» incluye la clase «españoles» en la clase de los «europeos», siendo la primera una subclase de la segunda.
Toda clase tiene la propiedad reflexiva (se incluye a sí misma) y la transitiva (si A está incluida en B y ésta en C, A está incluida en C).
La igualdad entre clases, que se escribe
[math]A = B[/math]
y se lee «la clase A es idéntica a B», afirma de ellas que una y otra tienen los mismos elementos. Así, por ejemplo, la clase de los números naturales pares es igual a la clase de números divisibles por dos.
El uso conjunto y combinado de los operadores de clase y las constantes de enunciados de clases (más las constantes de clase, como conjunto vacío y clase universal, además de los paréntesis) permite formar enunciados de lógica de clases. Aquellos enunciados de clases que son universalmente verdaderos, o que son tautológicos constituyen las leyes del cálculo de lógica de clases.
El álgebra de Boole es un cálculo basado en sólo dos operaciones de lógica de clases: la intersección y la unión de clases, y el recurso, además, a la clase complemento.
Lógica de relaciones
Desarrollo de la lógica de predicados que permite el estudio de la deducción en razonamientos que utilizan enunciados con predicados poliádicos, o predicados con más de un lugar, con los que se expresan relaciones entre dos o más individuos (binarias, ternarias, n-arias). Esta lógica permite tratar argumentos como:
- A quien le gusta París le gusta también Roma. A Ana le gusta París
- Sólo ciudades bellas cargadas de historia le gustan a Ana
- _______________________________________________________
- Por tanto Roma es una bella ciudad cargada de historia
- Donde «x gusta a y» es una relación.
O el conocido de Augustus de Morgan:
- Un caballo es un animal
- ________________________________________________
- Por tanto, la cabeza de un caballo es la cabeza de un animal
- (donde «x es la cabeza de y» es una relación).
Bibliografía sobre el concepto
- Quintanilla, M., Fundamentos de lógica y teoría de la ciencia. Ed. Univ. Salamanca, Salamanca, 1981.
- Cohen, M y Nagel, E., Introducción a la lógica y al método científico (2 vols.). Amorrortu, Buenos Aires, 1979.
- Verneaux, R., Introducción general y lógica. Herder, Barcelona, 1989.
- Hodges, W., Logic. Penguin B., Londres, 1991.
Relaciones geográficas