Teoría de la lógica tradicional sobre el silogismo. La teoría es expuesta por vez primera en la obra de Aristóteles, Analíticos primeros, se desarrolla a lo largo de la Edad Media, en la filosofía escolástica, y su estudio y desarrollo constituye la parte más importante de la lógica antigua. Algunos filósofos, como Bacon, Descartes, J.S. Mill y otros, la han constituido en objeto preferente de sus críticas, por considerar que sus demostraciones son una mera petición de principio, pero no deja de ser la parte de la lógica más venerable y tradicional, en la que se han ejercitado la mayor parte de mentes ilustres y, puesta en relación con otras partes de la lógica, no deja de ser una de sus cuestiones más centrales. La lógica moderna, por otra parte, le ha dedicado sistemas axiomáticos formalizados.
Si se la contempla desde la perspectiva de la lógica de clases, un silogismo supone relaciones de inclusión e intersección entre tres clases: las representadas por el término sujeto, el término predicado y el término medio.
Si se la contempla desde la perspectiva de la lógica de enunciados, un silogismo es un condicional formado por la conjunción de las premisas que implican a la conclusión.
Si se la contempla desde la perspectiva de la lógica cuantificacional, un silogismo categórico es un razonamiento compuesto por enunciados cuantificados (por los cuantificadores «todos» y «algunos», o generalizador y particularizador) que implican la conclusión.
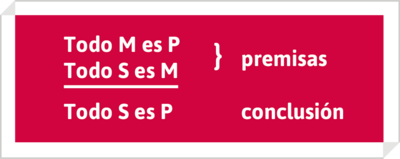
Como lógica de predicados, o de términos, analiza la estructura de conjuntos de enunciados compuestos de sujeto, cópula verbal y predicado, que constituyen razonamientos. El razonamiento basado en enunciados categóricos se llama silogismo categórico, compuesto por dos premisas y una conclusión. Las premisas contienen, además del sujeto y el predicado, un término común a ambas, o medio, mientras que la conclusión se compone del sujeto de una de las premisas y del predicado de la otra, desapareciendo el término medio
- Ningún cuadrúpedo sabe silbar
- Algunos gatos son cuadrúpedos
- ________________________________________
- Algunos gatos no saben silbar (L. Carroll)
- Ningún fósil puede estar traspasado de amor
- Una ostra puede estar traspasada de amor
- ____________________________________
- Las ostras no son fósiles (L. Carroll)
En un silogismo, como el siguiente :
- Todos los hombres son mortales
- Los filósofos son hombres
- _______________________________________
- Por tanto, los filósofos son mortales
se observa el siguiente esquema lógico:
donde S, «filósofos», es el término sujeto, P, «mortales», el término predicado y M, «hombres», el término medio.
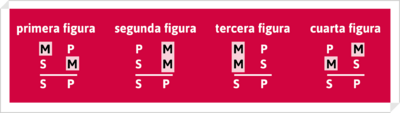
Según el lugar que ocupa el término medio, se distingue cuatro figuras del silogismo
Y dado que cada uno de los enunciados categóricos, que componen las premisas y la conclusión, puede variar según la cantidad y la cualidad, esto es, pueden ser universales o particulares y afirmativos o negativos, las cuatro figuras dan un total de 256 combinaciones posibles, o modos, de los cuales sólo 19 se consideran silogismos válidos o correctos
De la primera figura:
- Todas las criaturas zumbantes son molestas
- Todas los mosquitos son zumbantes
- __________________________________
- Todas los mosquitos son molestos
De la segunda figura:
- Todos los que cantan como canarios son melodiosos
- Ningún cisne es melodioso
- ___________________________________________
- Ningún cisne canta como un canario
De la tercera figura:
- Todos los leones son reyes de la selva
- Algunos leones son exhibidos en el circo
- ________________________________________________
- Algunos animales exhibidos en el circo son reyes de la selva
De la cuarta figura:
- Ningún fósil canta canciones románticas
- Alguien que canta canciones románticas es sensible
- ___________________________________________
- Alguien sensible no es un fósil
Recordando que los tipos de enunciados categóricos se ejemplifican mediante las letras A, E, I y O, los modos válidos son los siguientes:
La validez de los silogismos exige la observancia de diversas reglas:
1. Por lo menos una premisa ha de ser afirmativa
2. Si una premisa es negativa, la conclusión ha de ser negativa.
3. Si una premisa es particular, la conclusión ha de ser particular.
4. El término medio ha de ser universal por lo menos una vez.
5. Si un término es universal en la conclusión, lo ha de ser también en la premisa correspondiente
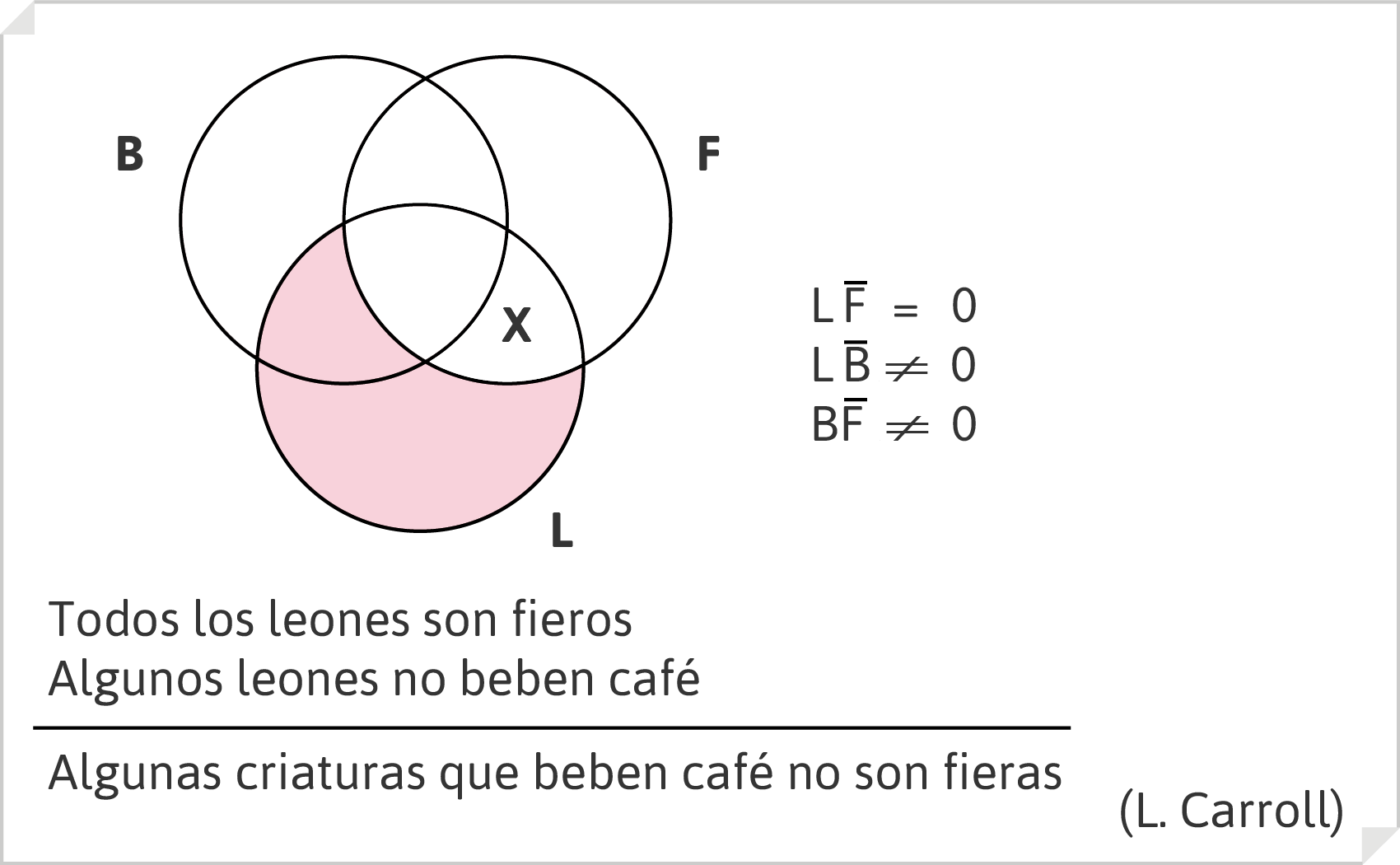
En el ejemplo de Lewis Carroll:
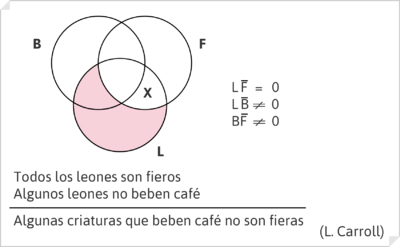
- Todos los leones son fieros
- Algunos leones no beben café
- _____________________________________________
- Algunas criaturas que beben café no son fieras
La conclusión es incorrecta (debería ser «algunas criaturas fieras no beben café») porque no cumple con la regla 4: un término que se toma en su acepción universal en la conclusión («no son fieras»), se ha tomado como particular en la premisa mayor.
La conclusión correcta tendría que ser:
«Algunas criaturas fieras no beben café».
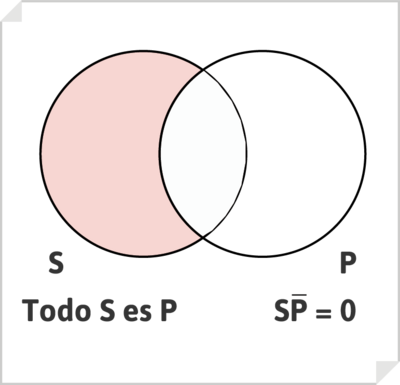
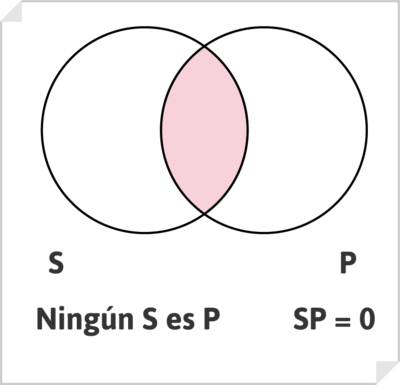
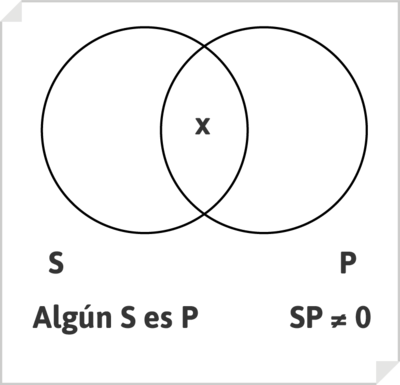
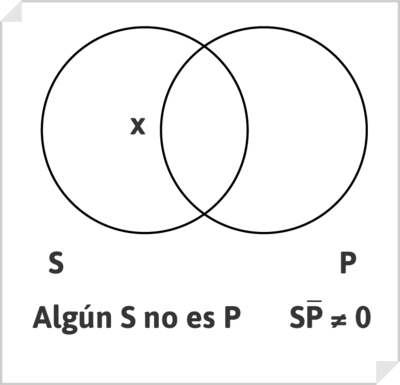
Puesto que los términos, sujeto y predicado, de un enunciado designan clases, un silogismo puede interpretarse como una relación entre clases; sus enunciados pueden representarse mediante los diagramas de Venn
, y la cuestión de la validez de los razonamiento silogísticos puede resolverse mediante estos mismos diagramas
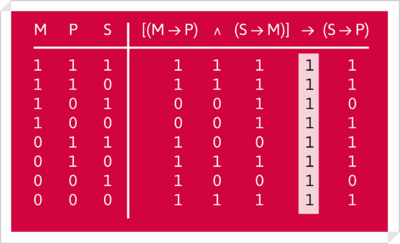
Si contemplamos los silogismos desde la perspectiva de la lógica de enunciados, pueden considerarse como una implicación, cuyo antecedente es una conjunción. Su validez, en este caso, puede demostrarse con las tablas de verdad:
Así, el ejemplo antes propuesto es una tautología :
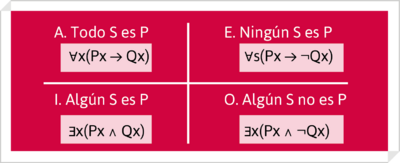
Los enunciados categóricos pueden ser también vistos desde la lógica de cuantificadores, pasando a adquirir la siguiente forma lógica:
En este caso, la validez de los silogismos se resuelve recurriendo a la lógica cuantificacional o lógica de cuantores
El silogismo de la primera figura:
- Todas las criaturas zumbantes son mal acogidas
- Todos los mosquitos son zumbantes
- _____________________________________
- Todos los mosquitos son mal acogidos
puede resolverse de la siguiente manera:
El silogismo de la segunda figura:
- Todos los que cantan como canarios son melodiosos
- Ningún cisne es melodioso
- ___________________________________________
- Ningún cisne canta como un canario
puede escribirse como:
El silogismo de la tercera figura:
- Todos los leones son fieros
- Algunos leones son exhibidos en el circo
- _________________________________
- Algunos animales exhibidos en el circo son fieros
puede escribirse de la siguiente manera:
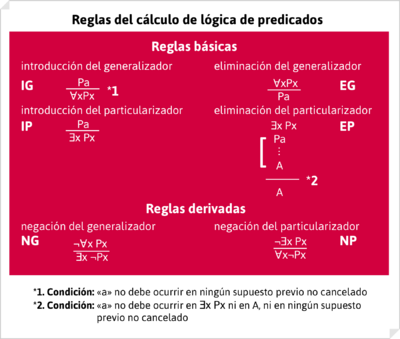
Al eliminar el particularizador en la línea 4, debe iniciarse una subderivación que permita introducir, como sucede en la línea 9, el cuantificador existencial. Así se cumple la condición *2, de las reglas del cálculo de la lógica de predicados (ver las reglas al final).
El silogismo de la cuarta figura:
- Ninguna fábula es terrible
- Hay cosas terribles que son seductoras
- __________________________________
- Hay cosas seductoras que no son fábulas
puede escribirse de la siguiente manera:
Al eliminar el particularizador en la línea 4, debe iniciarse una subderivación que permita introducir, como sucede en la línea 9, el cuantificador existencial. Así se cumple la condición *2, de las reglas del cálculo de la lógica de predicados (según las reglas que se muestran a continuación).
Relaciones geográficas