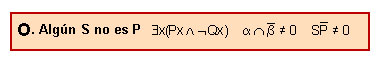Método gráfico, ideado por el lógico inglés John Venn, que permite representar las relaciones de clase existentes entre los términos de los enunciados categóricos y solucionar, de un modo fácil e intuitivo, la validez de los razonamientos silogísticos.
Diagramas
Un rectángulo representa el universo del discurso, U, y un círculo en el interior del universo representa una clase o un término, que se afirma en este universo, determinando dos zonas: la zona interior del círculo, en que están, o pueden estar, los elementos de esta clase, y la zona exterior al círculo donde están los elementos de la clase complemento :
Un círculo puede estar simplemente dibujado, o afirmado, rayado o coloreado, esto es vacío de elementos, y demás puede intersecar con otro círculo, representando de este modo un enunciado categórico. En este caso, se asignan letras mayúsculas S,P,Q,, ..., a cada círculo; las letras representan clases o términos:
La representación de dos círculos intersecantes determina la creación de cuatro tipos de zonas:
La zona 1: donde están los elementos de S, pero no de P.
La zona 2: donde están los elementos de S y P.
La zona 3: donde están los elementos de P, pero no de S.
La zona 4: donde están los elementos que no son ni S ni P.
___________________________________________________________________________________
Representación gráfica de enunciados categóricos
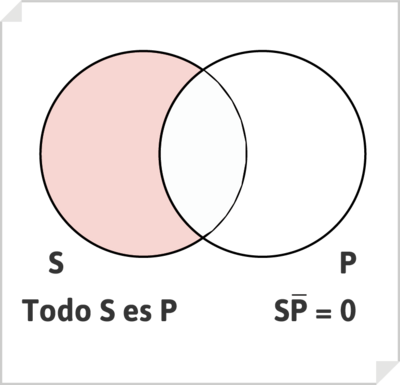
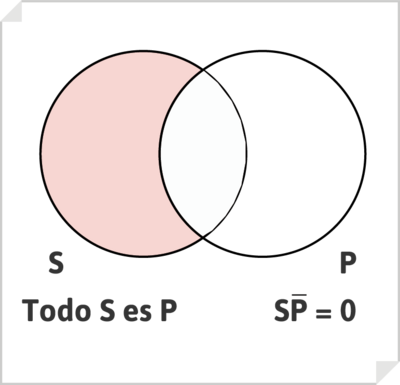
El enunciado categórico universal afirmativo, de tipo A, por ejemplo, «Todos los hombres son iguales», se representa mediante la intersección de dos círculos, vaciando (rayando o coloreando) la zona correspondiente a .
donde el enunciado «Todos los hombres son iguales» debe interpretarse como «Nada que sea hombre no es igual», o «No hay S que no sea P».
___________________________________________________________________________________
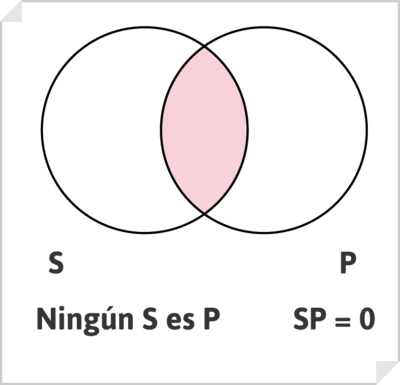
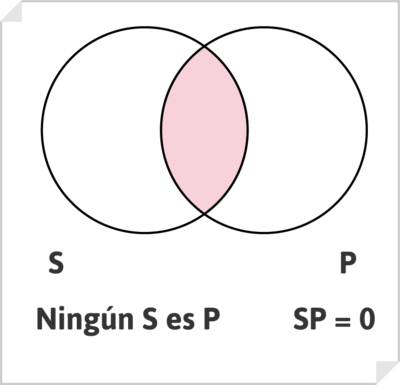
El enunciado categórico universal negativo, de tipo E, como por ejemplo, «Ningún hombre es inmortal», se representa vaciando (rayando o coloreando) la zona de intersección correspondiente a SP = 0.
donde el enunciado «Ningún hombre es inmortal» debe leerse como «Nada es hombre e inmortal a un tiempo», o «No hay S y P a un tiempo».
___________________________________________________________________________________
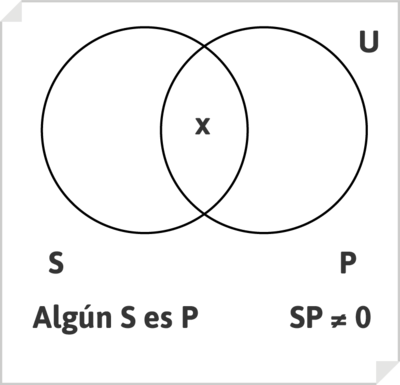
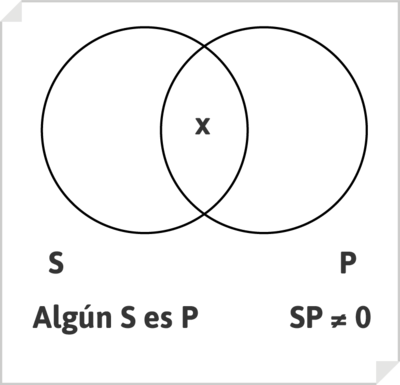
El enunciado categórico particular afirmativo, de tipo I, por ejemplo, «Algunos hombres son sabios», se representa afirmando que la zona de intersección de S y P no es vacía: que existe, por lo menos, un elemento de la misma, que dibujamos marcando con una X.
de modo que el enunciado «Algunos hombres son sabios» debe leerse como «Hay hombres que son sabios», o «Hay S y P a un tiempo».
___________________________________________________________________________________
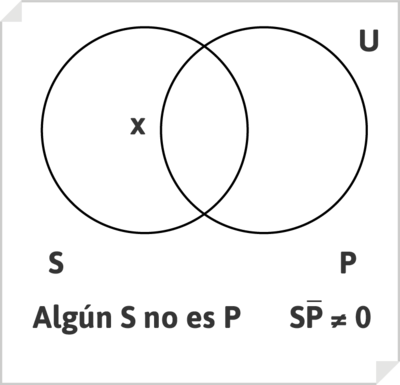
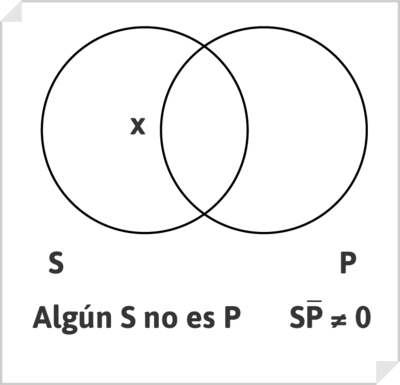
El enunciado categórico particular negativo, de tipo O, por ejemplo, «Algunos hombres no son libres», se representa afirmando que no es vacía la zona formada por los elementos que son S y no P a un tiempo: que en tal zona existe por lo menos un elemento de la misma, que dibujamos marcando con una X.
de modo que el enunciado «Algunos hombres no son libres» se lee como «Hay hombres que no son libres», o « Hay S y no P a un tiempo»
___________________________________________________________________________________
Ejemplos
[math]\alpha \cap \overline{\beta}= 0[/math]
Todo S es P
Ningún S es P
[math]\alpha \cap \beta= 0[/math]
Algún S es P
[math]\alpha \cap \beta \neq 0[/math]
Algún S no es P
[math]\alpha \cap \overline{\beta} \neq 0[/math]
___________________________________________________________________________________
Representación gráfica de los silogismos
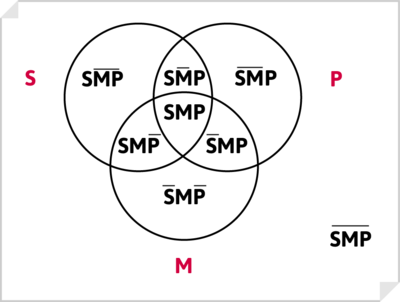
En los razonamientos silogísticos los enunciados componentes son tres, por tanto el universo queda dibujado de la siguiente manera:
Los tres círculos correspondientes a los términos, S, P y M, delimitan ocho zonas que representan su extensión: cuatro zonas de intersección y cuatro zonas de no intersección. Cada enunciado del silogismo, ya sea premisa o conclusión, afirma algo sobre algunas de estas zonas.
Se considera válido aquel silogismo en que ocurre que, al dibujar las premisas, queda ya dibujada la conclusión.
___________________________________________________________________________________
Ejemplo:
Sea el siguiente silogismo:
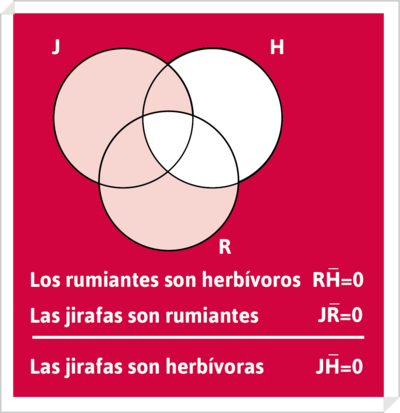
- Los rumiantes son herbívoros
- Las jirafas son rumiantes
- _____________________________
- Las jirafas son herbívoras
Para comprobar su validez:
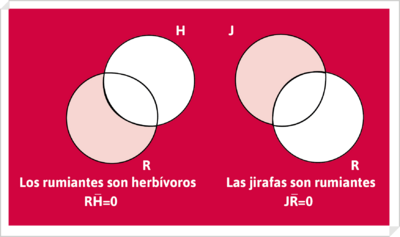
(1) dibujar sucesivamente ambas premisas sobre el mismo universo:
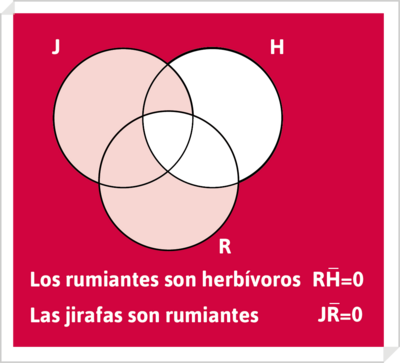
de modo que constituyan un solo diagrama :
(2) Comprobar que la conclusión queda ya dibujada en el diagramas de las premisas:
___________________________________________________________________________________
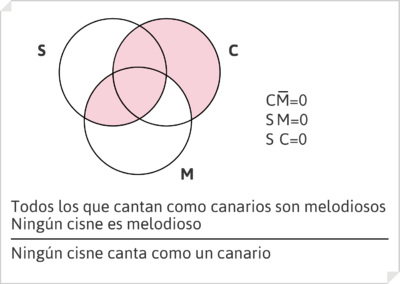
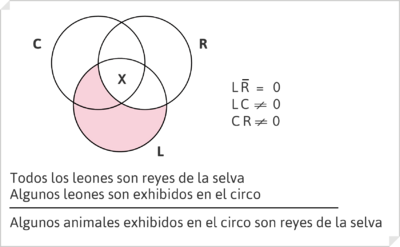
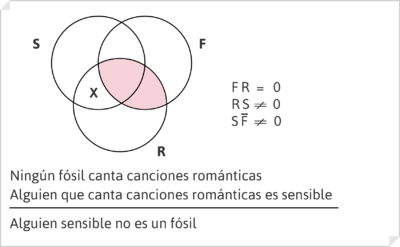
De la misma manera, con igual método es posible comprobar gráficamente la invalidez de algunos razonamientos silogísticos.