Símbolo que se aplica a los enunciados que corresponden a las denominadas proposiciones categóricas universales afirmativas de la lógica clásica.
Son enunciados del tipo «Todos los S son P», en los que S es el término sujeto y P el término predicado, con la cantidad universal y la cualidad afirmativa. Muchas son las maneras de formular esta clase de enunciados:
Todo lo que es S es P
Todo S es P
Lo S es P
Cada S es P
Aquello que es un S es un P
Si algo es S, es P
Si S, P
Si algo es S entonces es P
Sólo si es P es S
Nada que no sea P es S
Nada es S si no es P
No hay ningún S que no sea P
No hay S que no sea P
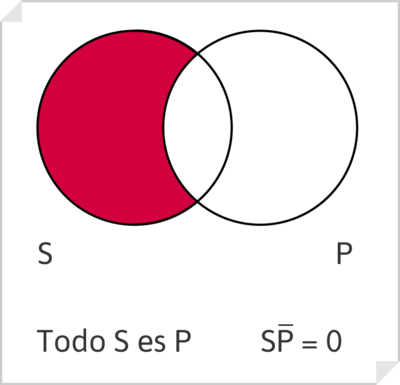
Los enunciados tipo A junto con los del tipo I (particulares afirmativos) forman el grupo de los enunciados afirmativos (del latín affirmo provienen precisamente los símbolos A e I correspondientes). Los enunciados tipo A se dibujan de la siguiente manera, con los diagramas de Venn:
donde la región [math]S\overline{P}[/math] es vacía, puesto que se afirma que todo S pertenece a P.
Según la interpretación de la lógica tradicional, se supone que el término sujeto denota, por lo que debe existir algún término S en la zona SP (mientras que no hay información acerca de si lo hay también en la zona [math]\overline{S}P[/math]
Según la interpretación que la lógica moderna hace de estos enunciados, no debe entenderse que «Todo S es P» implica que existe algún S, por lo que la forma correcta de entender estos enunciados es «Si existe algún S, entonces es P».