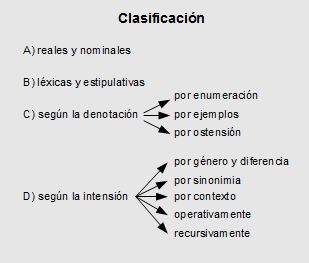
En este cuadro se muestran los distintos tipos de definición que, a su vez, son maneras distintas de definir. Una primera división distingue las definiciones en reales y nominales. Una definición es real si su definiendum es un concepto, cuya esencia ha de precisarse en el definiens. (Ver ejemplo ↓)
Definición real:
«Un triángulo es una figura plana y cerrada, formada por tres líneas que se cortan dos a dos».
Se dice «real» porque quiere referirse a la esencia de la cosa tal como es y, en su deficiencia (no se definen cosas), al concepto que ocupa el lugar de la cosa.
Una definición es nominal si se define el uso de un término. (Ver ejemplo ↓)
Definición nominal:
«"Cosmología" es la ciencia que trata del origen del universo».
Se trata de una clasificación tradicional, muy utilizada antiguamente, pero ya abandonada porque se basa en criterios metodológicos aristotélicos poco científicos.
Las definiciones pueden también distinguirse en léxicas y estipulativas. Una definición léxica es aquella que precisa el significado usual de un término tal como se utiliza en una comunidad lingüística (tal como aparece en el diccionario, o léxico. (Ver ejemplo ↓)
Definición léxica:
Cualquier definición del diccionario de la lengua es un ejemplo de definición léxica.
Una definición estipulativa es aquella que convencionalmente se decide por razones de claridad y precisión en un contexto determinado. (Ver ejemplo ↓)
Definición estipulativa:
«Quisiera ser explícito sobre el significado que tiene para mí el término "mecanismo". Un mecanismo es cualquier proceso físico determinante. Un proceso abstracto constituye un mecanismo si, en principio, existen modos de realizarlo mediante un proceso físico. Así, cualquier programa de computador digital constituye un mecanismo»
A. Newell, Inteligencia artificial y el concepto de mente, Cuadernos Teorema, Valencia 1980, p. 89.
Según las maneras fundamentales de construir las definiciones, o la técnica utilizada, pueden distinguirse también varias clases. Las definiciones denotativas son aquellas en las que se recurre a la denotación de un término. Podemos recurrir a la denotación, o extensión, de un término: enumerando todos los objetos a los que se aplica significativamente un término (ver ejemplo ↓)
Definición por enumeración:
«"Escandinavos" = df los daneses, noruegos, suecos o islandeses».
,o dando ejemplos (Ver ejemplo ↓)
Definición por ejemplos:
«Un Estado plurinacional es, por ejemplo, España »
, o utilizando una definición ostensiva (ver ejemplo ↓)
Definición ostensiva:
«'Rojo' = df este color que vemos en esta bandera»
Las definiciones intensivas, por su parte, recurren a la intensión o comprensión de la palabra o término, esto es, al conjunto de características definitorias. Son diversas las maneras como se puede precisar la intensión de un término. Así, la definición por género y diferencia (Ver ejemplo ↓)
Definición por género y diferencia:
«El hombre es un animal racional»
que es la manera más tradicional de definir y, a la vez, una de las más frecuentes, enuncia las dos carácterísticas más generales del término, de las cuales una (diferencia) es la determinación de la otra, más general (género); la definición contextual, que supone la redacción de un contexto para el definiens, con el cual se aclara el uso o el significado del término definiendum (Ver ejemplo ↓)
Definición contextual:
«Llamamos 'término ambiguo' a aquel que, puesto en un contexto, no exluye todos los significados menos uno»
-muy usada esta definición en contextos científicos, emplea frecuentemente la expresión «si y sólo si» (Ver ejemplo ↓)
Definición en contextos científicos:
«Un suceso Y en un tiempo T es causado por un suceso precedente S si y sólo si es deducible de X con ayuda de las leyes LT conocidas en el tiempo T »
R. Carnap, Fundamentación lógica de la física, Buenos AIres, 1969, p. 257.
- la definición por sinónimos (Ver ejemplo ↓)
Definición por sinónimos:
«Osado, es decir, atrevido en exceso»
,en la que el definiens se compone de uno o varios términos totalmente equivalentes en significado uno a uno; y, por último, en contextos más bien científicos, la definición operacional, en la que el definiens describe que, si se ejecuta una operación, se producen una o varias características determinadas, que constituyen el significado del definiendum (Ver ejemplo ↓)
Definición operacional:
«'Sustancia soluble en el agua' = df aquella que, introducida en el agua se disuelve»
Uno de los tipos más utilizados en lógica y matemáticas es la definición recursiva:aquella en la que, dada la complejidad del definiendum, el definiens consiste en una serie de definiciones parciales, o en un sistema de definiciones, de modo que cada nuevo definiens, más complejo, recurre a los definiens anteriores, más simples y fundamentales, necesitando la definición final de todas las anteriores parciales para ser correcta. Se construye utilizando la recursividad, o procedimiento con que se aplica una operación repetidas veces. (Ver ejemplo ↓)
Definición recursiva (de fórmula)
(a) Toda fórmula atómica es una fórmula
(b) Si S es una fórmula, entonces ¬S es una fórmula
(c) Si S y R son fórmulas, entonces [math]R\wedge S, R\vee S, R\rightarrow{S} y R\leftrightarrow{S}[/math] son fórmulas
(d) Si R es una fórmula y x es cualquier variable, entonces [math] \forall{x} (R)[/math] y [math]\exists{x} (R)[/math] son fórmulas
(e) Ninguna expresión es una fórmula a menos que el que lo sea se siga de las reglas anteriores.
P. Suppes, Introducción a la lógica simbólica, CECSA, México 1980, p. 83-84.

