(del griego αναλογíα , analogía, correspondencia, proporción, derivado de ana lógon, según proporción, proporcional) Es la semejanza que se establece entre términos, conceptos o cosas que se comparan. Mediante la analogía, a veces entendida en sentido metafórico, pueden agruparse distintos conjuntos de cosas de los que se afirma una característica común por semejanza: el niño, el río, el vino o el vinagre y hasta la lengua tienen todos «madre»; el aspecto, el clima o el alimento son «sanos», pero en un sentido que a la vez coincide y que difiere, aunque en realidad todo predicado ha de entenderse analógicamente, cuando no se hace abstracción de la realidad: hablar de la vida vegetal y de la vida animal es un uso analógico del término, que se aplica en realidad de forma distinta a un vegetal o a un animal. El concepto cuya analogía ha sido objeto de tratamiento específico en filosofía es el de ser. La proporción a que se refiere la etimología, y que ha fundamentado su uso tanto en el lenguaje ordinario como en el filosófico, es la proporción matemática, llamada propiamente geométrica, que se expresa según la secuencia a:b::b:c, en la que el primer término se refiere al segundo igual como éste al tercero; cada uno de estos términos se llama analogado; la relación o proporción, cuantitativa en origen, pasó luego a ser cualitativa.
El término procede de los escritos de los pitagóricos, donde significa proporción matemática (ver cita), concepto que aplican tanto a la armonía musical como a las magnitudes del cosmos.
Los primeros pitagóricos conocían las tres proporciones matemáticas siguientes
1) La proporción aritmética
[math]a-b=b-c \frac{a-b}{b-c}= \frac{a}{a}= \frac{b}{b}= \frac{c}{c}=1 b=\frac{a+c}{2}[/math]
«El primer término excede al segundo en la misma cantidad que éste excede al tercero»:
2) La proporción geométrica
«El primer término es al segundo como éste es al tercero»
[math]\frac{a}{b} = \frac{c}{d} b^2 = ac \frac{a-b}{b-c}= \frac{a}{b}= \frac{b}{c} b= \sqrt[2]{ac} [/math]
3) La proporción armónica
«Sea cual sea la parte de sí mismo en que el primer término excede al segundo, el segundo excede al tercero en una parte igual de este tercero»
[math]a = b+\frac{a}{n} b = c+\frac{c}{n} \frac{1}{c}-\frac{1}{b}= \frac{1}{a} \frac{a-b}{b-c}= \frac{a}{c} b= \frac{2ac}{a+c}[/math]
A.Pichot, La naissance de la science, 2 vols., Gallimard, París 1991, vol. 2, p. 143
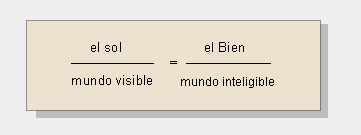
Platón utiliza la noción de analogía como proporción (matemática) para explicar sobre todo la función del Bien en su teoría fundamental de los dos mundos («lo que es el sol en el mundo visible es el bien en el mundo invisible»; (ver cita), así como para señalar el grado de claridad y verdad que poseen los segmentos a que se refiere la metáfora de la línea (ver texto ). Aristóteles, además de utilizarla como método comparativo en ética y biología -iniciando así el uso del argumento de analogía- funda la teoría de la analogía del ser (ver texto), que se convertirá en punto fundamental de la metafísica de la filosofía escolástica medieval, que establece una relación metafísica u ontológica, por lo mismo de algún modo real, entre los analogados. Tras perder esta carga metafísica, no tiene en la actualidad la analogía más que usos muy específicos en campos determinados del pensamiento, como la lingüística (metáfora), la biología (analogía-homología) o la lógica (isomorfismo, modelos, argumento de analogía).
Las analogías que establece Platón entre el sol y el Bien pueden verse en la siguiente tabla, que abarca las características del Sol y del Bien, del mundo inteligible y del mundo sensible, descritas en Platón, La república, 508-509:
_________________________________________________________________________________
Cf. Platón, La République, trad. y notas de R. Baccou, Flammarion, París 1968, n. 437, p. 436
Bibliografía sobre el concepto
- Beuchot, M., Hermenéutica, analogía y símbolo. Herder, México, 2015.
- Beuchot, M., Hermenéutica, analogía y símbolo. Herder, Barcelona, 2015, 2 ed.
- Beuchot, Mauricio, Hermenéutica, analogía y símbolo. Herder, México, 2004.
- Monatgnes, Bernard, L'analogie de l'être d'après Saint Thomas d'Aquin. Cerf, Paris, 2008, 2 ed.
- Igual, Vicent, La analogía. PPU, Barcelona, 1989.
- Seguró, M., Los confines de la razón. Analogía y metafísica trascendental. Herder, Barcelona, 2013.
- Seguró, M., Sendas de finitud. Analogía y diferencia. Herder, Barcelona, 2015.
- Beuchot, Mauricio, Tratado de hermenéutica analógica. Ítaca-UNAM, México, 1997.

