Famoso texto de Platón que aparece al final del libro VI de la República (509d-511e) en el que se expone las relaciones entre el mundo sensible y el mundo de las ideas, y señala los diversos grados de conocimiento, a la vez que sugiere el camino y la misión de la dialéctica. Es, pues, un texto en el que se trata del auténtico conocimiento filosófico, del papel de las hipótesis y de las articulaciones entre los distintos niveles ontológicos y epistemológicos ([#linea ver el texto de la metáfora de la línea] ). La continuación de este texto es el celebérrimo texto del mito de la caverna, que se desarrolla en el libro VII de la misma obra.
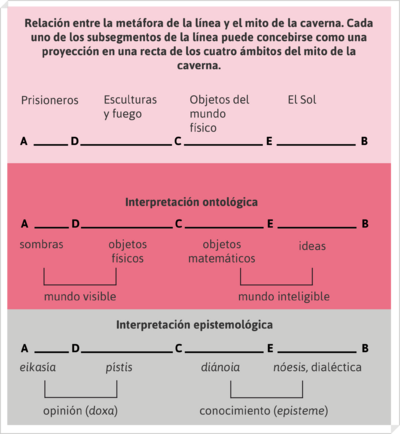
En la metáfora de la línea, Platón propone que tracemos una línea AB y que la dividamos en partes desiguales por el punto C, de esta forma obtenemos dos subsegmentos: el AC y el CB, siendo el primero de ellos más corto que el segundo. Acto seguido Platón propone que consideremos el segmento más corto como si se tratase de una imagen o copia del segmento CB y, por tanto, más imperfecta (de la misma manera que una copia es inferior al original, o que una sombra o un reflejo tienen una existencia dependiente del objeto del cual son sombra o reflejo), de ahí que la represente con una longitud menor. Posteriormente, asigna a cada uno de los segmentos la representación de distintos grados de la realidad y de distintos grados del conocimiento. De esta manera, nos introduce en sus tesis de una gradación de la realidad en la que cabe considerar distintos grados de imitación o representación de las ideas, así como distintos grados y caminos de conocimiento. A su vez, dice, dividamos cada uno de estos dos segmentos mediante los puntos D y E, siguiendo la misma proporción. De forma que:
AD/DC = CE/EB y, en general, como AC/CB.
Así obtendremos una línea dividida en 4 segmentos tal como:
desde una perspectiva ontológica:
mundo sensible mundo inteligible
/ \ / \
sombras obj. físicos entes matemáticos ideas
A_______D__________C______________E_____________________B
eikasía pístis dianoia noesis dialéctica
\ / \ /
opinión (doxa) conocimiento (episteme)
desde una perspectiva epistemológica:
Punto de vista ontológico
El segmento mayor CB representa, desde el punto de vista ontológico, el mundo inteligible.
El segmento menor AC representa, el mundo sensible,
El segmento AC se subdivide en AD y DC, según la proporción AD/DC=AC/CB, indicando con ello que AD es la imagen de DC, como AC lo era de CB. De esta manera Platón, desde el punto de vista ontológico, sitúa en el subsegmento inferior AD las sombras y las imágenes de los objetos físicos reales que están representados por DC.
A su vez, el segmento CB también se subdivide según la misma proporción, de forma que CE representa, desde un punto de vista ontológico, los entes matemáticos.
El segmento EB representa los primeros principios, las ideas o formas
Todos los segmentos están relacionados entre sí, y respecto del segmento EB, por la relación «ser imagen de», o «ser representación de».
Punto de vista epistemológico
El segmento mayor CB representa, epistemológicamente, el conocimiento verdadero o episteme (ἐπιστήμη).
El segmento menor AC representa la doxa (δόχα) u opinión.
El segmento AC se subdivide en AD y DC, según la proporción AD/DC=AC/CB, indicando con ello que AD es la imagen de DC, como AC lo era de CB. De esta manera Platón, desde la perspectiva epistemológica AD representa la creencia o pístis (πίστις), y DC la imaginación o eikasía (εἰχασία).
A su vez, el segmento CB también se subdivide según la misma proporción, de forma que CE representa, desde un punto de vista epistemológico, el pensamiento discursivo o dianoia (διάνοια).
El segmento EB representa la razón intuitiva o noesis (νόεσις) que se desarrolla dialécticamente.
Todos los segmentos están relacionados entre sí, y respecto del segmento EB, por la relación «ser imagen de», o «ser representación de».
El aspecto más interesante de esta metáfora no estriba tanto en la relación general entre AC y CB (mundo sensible y mundo inteligible), que Platón desarrolla de manera más completa en otros textos (como en el mito de la caverna, por ejemplo), sino en la relación establecida entre DC y CE, por una parte, y la relación entre CE y EB, por otra. En estas relaciones se pone de manifiesto la admisión por parte de Platón de los entes matemáticos (a los que, según Aristóteles, tanta importancia daba Platón (ver texto ) situados en CE, que se valen de los objetos físicos como si éstos fuesen imágenes de aquéllos y, a su vez, son como imágenes de las auténticas ideas (EB), ocupando un lugar intermedio entre los objetos de la realidad física y el mundo de las ideas. La existencia de estos entes es la que permitiría a Platón dar un fundamento a las matemáticas y evitar el problema suscitado por la afirmación de la existencia de diversos círculos, triángulos y, en general, la iteración.
¿Cómo explicar la posibilidad de intersecciones entre círculos, triángulos, iteraciones repetidas del «mismo» número, etc., si solamente hubiese una única idea de circunferencia, de triángulo, de número tres, etc.? Para solucionar este problema, Platón sitúa en CE los entes matemáticos, copias perfectas de las ideas, pero plurales y no idénticas a ellas, que actuarían como intermediarios entre las verdaderas ideas y la realidad sensible. Por una parte ya son objeto del conocimiento científico (episteme), pero todavía no son objeto de la forma superior de este (la noesis). Por ello, solamente son objeto de la intelección o pensamiento discursivo (dianoia). Platón también afirma que la ciencia que corresponde a CE se sustenta en hipótesis y presupuestos que ella misma no estudia, y es tarea del conocimiento situado en EC, es decir, de la filosofía, el estudio de estos primeros principios y presupuestos absolutos. Así, el segmento que, desde el punto de vista ontológico, representa los entes matemáticos, se corresponde con la dianoia. La dianoia tiene como objeto de estudio aquello que el alma se siente impulsada a estudiar con ayuda de las imitaciones de los primeros segmentos. De la misma manera que el subsegmento DC es el modelo que copia el subsegmento AD, el subsegmento CE es el que sirve de modelo al mismo DC.
Si se compara este texto con la famosa alegoría de la caverna que se desarrolla un poco más adelante en el comienzo del libro VII de la República (514a-517e) (ver el texto del mito de la caverna ), también puede señalarse que cada uno de los segmentos de la línea se corresponden con las cuatro grandes regiones en las que se divide la realidad descrita por este mito. También en la caverna pueden distinguirse dos grandes regiones: la del interior de la caverna, y la del exterior. La caverna, a su vez, está poblada por entidades que son manifiestamente copias del exterior y, en ella, se distingue la región en la que están encadenados unos prisioneros obligados a observar solamente sombras y la región que ocupan unos misteriosos personajes que llevan esculturas iluminadas por un fuego. Pero si las sombras lo son de las esculturas, el fuego del interior de la caverna es sólo una muy imperfecta imitación de la luz del sol que está en el exterior. Así, AC se corresponde con el interior de la caverna y CB con el exterior; AD con las sombras que ven los prisioneros y con éstos mismos; DC con las figuras proyectadas por el fuego de la caverna, de las cuales las sombras son su proyección; CE con el mundo exterior del cual todo cuanto está en la caverna es mera copia y EB con el sol, sin el cual, como sin las ideas, nada de cuanto hay en los otros ámbitos de lo real podría ser ya que, como dice Platón, en cierto modo, al igual que el sol es la causa de las estaciones, de la distinción entre el día y la noche y de la existencia de vida sobre la tierra, las ideas y, en especial, la idea de Bien es la causa suprema.