(deriva del latín «fractus»: roto, irregular, y sugiere también lo fraccional y fragmentario)
Designa una entidad geométrica creada por el matemático Benoit B. Mandelbrot, que consta de fragmentos geométricos de orientación y tamaño variable aunque de aspecto semejante, de manera que, si lo ampliamos (o reducimos), aunque cambie la escala, se muestra como una serie repetitiva de niveles similares. Es decir, que posee la propiedad de la autosimilitud o sibisemejanza, obtenida por un proceso de iteración repetida de unas formas que se van autorreplicando.
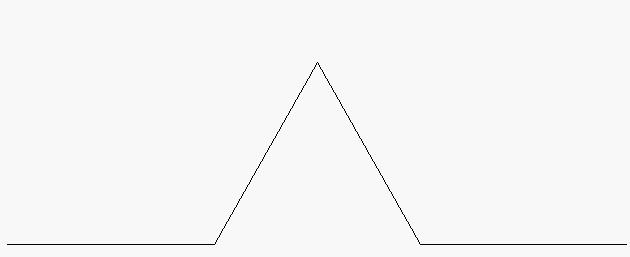
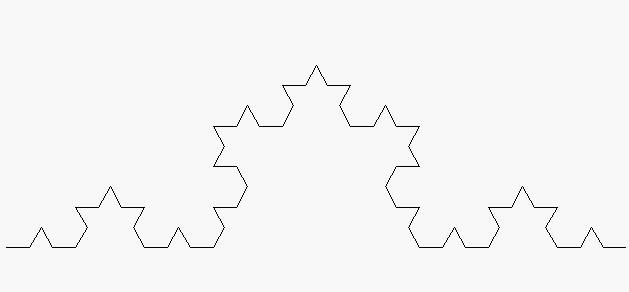
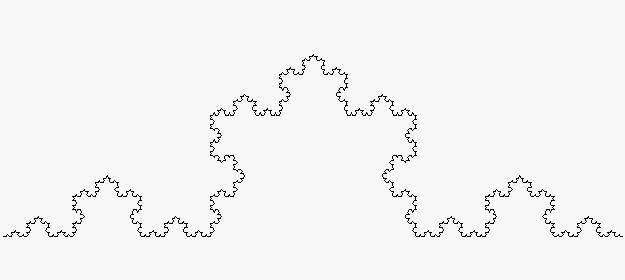
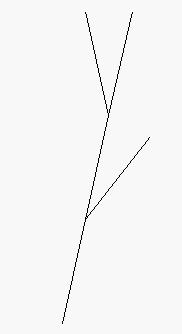
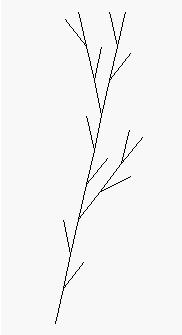
La geometría fractal tiene sus antecedentes en la obra de algunos matemáticos del siglo XIX, tales como Koch, Cantor, Peano, Hilbert, Sierpinski, y otros, que ya estudiaron desde las singularidades de curvas no derivables, hasta la formación recursiva de determinadas formas geométricas, como la curva de Peano (ver imagen), la curva de Hilbert (ver imagen), la curva de H. von Koch (conocida como «copo de nieve», ver imagen), la «alfombra» de Sierpinski, o la «esponja» de Menger (entidades matemáticas que tienen una área finita pero un perímetro infinito, o una superficie infinita pero un volumen nulo). Pero se debe a Mandelbrot el pleno desarrollo de esta nueva geometría que se aplica al estudio de numerosos fenómenos relacionados con la teoría del caos, tales como el estudio de: formas naturales no descriptibles mediante geometrías convencionales, la forma de las líneas costeras, la formación de montañas, la forma de las nubes, de los polímeros, las circunvoluciones cerebrales, la formación y ramificación de las estructuras pulmonares, la ramificación de árboles y arbustos (ver imagen), el estudio de patrones meteorológicos, y los procesos de la morfogénesis biológica. Además, aplicando la geometría fractal, se han creado algoritmos de compresión y de generación de imágenes de gran aplicación en informática, en vídeo y en cinematografía.
La aplicación de la geometría fractal permite entender los sistemas complejos de la naturaleza, que parecen preservar y recapitular el aspecto de los detalles en escalas cada vez más finas, lo que sugiere principios o patrones de crecimiento y de forma regidos por leyes matemáticas similares y, por tanto, aplicables a múltiples ámbitos de investigación. Esta geometría, como la teoría de las catástrofes de René Thom, ha revitalizado aspectos cualitativos en la matemática, y se incardina en un proceso de renovación holística de la ciencia.
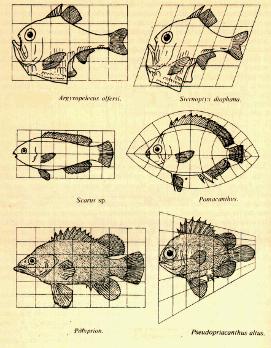
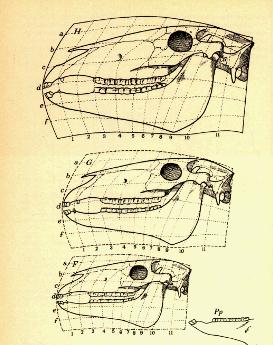
Según Mandelbrot, la geometría fractal, como la teoría de la relatividad o la mecánica cuántica, descubre una interdependencia entre el sujeto y el objeto en el proceso de medición, ya que el objeto medido depende de las escalas utilizadas por el observador. Con ello, la noción de magnitud se relativiza y se pone en función de la escala o perspectiva del observador. Así, en lugar de las magnitudes cuantitativas, Mandelbrot propone una medida cualitativa de dimensiones fractales que expresa el grado de complejidad relativa de un objeto. Además, pone en entredicho la creencia según la cual las formas complejas han de estar generadas por procesos complejos, ya que los fractales, a pesar de su gran complejidad, pueden generarse por iteraciones sucesivas de formas simples. Se pueden obtener formas fractales muy complejas repitiendo una transformación geométrica simple, y pequeños cambios en los parámetros de esta transformación, provocan cambios globales. Esto permite abordar desde una perspectiva nueva (aunque ya entrevista por d'Arcy Thomson a principios de siglo (ver imágenes) el estudio de la morfogénesis, y permite aplicar la geometría fractal al estudio de la transmisión genética. Pero, como ya hemos dicho anteriormente, el ámbito de aplicación de la teoría de los fractales es muy amplio: desde la economía, hasta la cosmología; desde la física de fluidos, hasta la cartografía. De esta manera, la geometría fractal aparece como una teoría descriptiva general del cambio que es independiente del substrato que lo origina.
Aunque en una estructura fractal domina la autosemejanza, no hay propiamente autoidentidad. Se verifican cambios: cada parte de una figura fractal es una imagen replicada de la totalidad, una especie de microcosmos que replica a su escala el macrocosmos al que pertenece, pero con variaciones. Esta estructura holística se asemeja también a la de los hologramas que, al dividirse o cortarse, reproducen la figura completa. Con ello, parecen recuperarse algunos antiguos modelos holísticos del mundo pero, lejos de la mera especulación, se fundan en sólidas investigaciones que ofrecen un sistema descriptivo de gran potencia y permiten esbozar nuevas metodologías de investigación de la complejidad de la naturaleza.