Conectiva diádica que opera entre dos enunciados o dos letras de enunciado. Se simboliza como
y se lee «P si y sólo si Q».
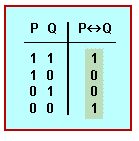
Su sentido se precisa con su definición mediante la tabla de verdad:
[math]"P\leftrightarrow{Q}"[/math] es verdadero cuando [math]P[/math] y [math]Q[/math] son ambos verdaderos, en los demás casos es falso» (ver ejemplo).
Ejemplo
Si p = eres feliz» y q = «amas», el enunciado «eres feliz si y sólo si amas», o «eres feliz siempre y cuando ames» es verdad cuando «eres feliz y amas» y cuando «ni eres feliz ni amas», pero es falso si es verdad una de ambas cosas y no la otra.
Dos enunciados cualesquiera, p y q, unidos por esta conectiva diádica se leen de diversas maneras, con sentido no obstante idéntico:
[math](p\leftrightarrow{q})[/math]
puede leerse como: «p si y sólo si q», «si p entonces q y si q, entonces p», «p es condición necesaria y suficiente de q», «p equivale a q», «si p entonces q y si no p, entonces no q»
Ejemplo
[math](p\rightarrow{q})\wedge (q\rightarrow{p})[/math]
Su tabla de verdad es equivalente a la de
[math](p\leftrightarrow{q})[/math]
[math](p\rightarrow{q})\wedge (¬q\rightarrow{¬p})[/math]
Su tabla de verdad es equivalente a la de
[math](p\leftrightarrow{q})[/math]