(ταυτολογία del griego τάυτό, tautó, lo mismo, y λόγος, logos, término)
Literalmente, decir lo mismo dos veces. En sentido amplio, toda proposición analítica o todo enunciado (explícitamente) analítico, es decir, cualquiera de aquellos enunciados analíticos que lo son en virtud de su forma, no por el significado de sus términos.
En sentido estricto, es una verdad lógica, o una verdad formal, o aquel esquema lógico o aquella forma lógica, cuyos ejemplos de sustitución son todos verdaderos.
En sentido amplio, es una tautología decir que «los ladrones son amantes de lo ajeno», porque es una verdad analítica, pero es una tautología estricta decir que «un hogar es siempre un hogar», porque es un ejemplo de sustitución de un esquema formal que, en lógica de enunciados, se escribe [math]p\rightarrow{p}[/math]
Ejemplo
«Venceremos o no venceremos» es una tautología, que puede escribirse
[math]q\vee ¬q[/math]
y es por tanto verdadera por su forma lógica; en cambio, «Eres padre, si eres varón mientras que eres madre, si eres mujer» es un enunciado analítico no tautológico.
Las tautologías son verdades lógicas y su negación constituye una contradicción (ver texto ).
En el cálculo lógico de enunciados, una fórmula es tautológica si es verdadera para cualquier asignación de valores de verdad, o para cualquier interpretación.Igualmente, la negación de una fórmula tautológica es una contradicción.
Ejemplo
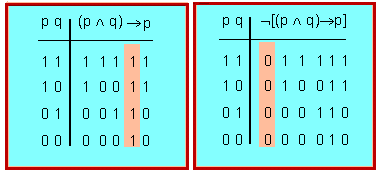
[math](p\wedge q) \rightarrow{p}[/math]
es una tautología;
[math]¬[(p\wedge q) \rightarrow{p}][/math]
es una contradicción.