Ésta podría ser una edición anterior y no la más reciente o aprobada. Ir a la versión actual.
Primeras paradojas de la historia del pensamiento, atribuidas a Zenón de Elea, y transmitidas sobre todo a través de la Física de Aristóteles. Discípulo de Parménides, hasta hijo adoptivo o quizá amante, Zenón divulgó la idea de la imposibilidad del movimiento, o del cambio, mediante diversos razonamientos sofísticos y argumentaciones paradójicas, de las cuales las más conocidas son cuatro (pero, al parecer, llegaron a ser más de cuarenta), basadas todas ellas en el argumento (o argumentos) contra la pluralidad: la paradoja de Aquiles y la tortuga, la paradoja de la dicotomía, la de la flecha en vuelo, y la paradoja del estadio.
Contenido
Argumento contra la pluralidad
Zenón se opone a la pluralidad y a la divisibilidad de las cosas, tal como la entendían los pitagóricos, con diversos argumentos, transmitidos por fragmentos conservados, sobre todo, en la Física de Aristóteles y los Comentarios a la física de Aristóteles de Simplicio. Tanto el espacio como las cosas mismas no pueden ser ni divisibles ni plurales; a los ojos de la razón no existen «muchas» cosas, y todo es «uno». En efecto, las cosas no son divisibles, porque, si lo fueran, o estarían formadas por elementos infinitamente divisibles e inextensos o de un número finito de elementos extensos. En el primer caso, la cosa misma entera carecería de extensión, porque lo infinitamente pequeño -según Zenón, que desconocía la suma finita de una serie de valores infinitamente pequeños- es igual a cero. En el segundo caso, la cosa entera misma sería infinitamente grande, porque, ¿qué puede separar dos elementos finitos? Otros elementos finitos. Y éstos, a su vez, ¿cómo pueden separarse? Por otros elementos finitos, y así hasta el infinito (no se conocía aún el vacío). Infinito número de elementos finitos separados dan un total, para cualquier cosa, de dimensiones infinitas. El argumento tiende a mostrar que, supuesta la pluralidad y la divisibilidad, se llega a conclusiones contrarias (elementos finitos, elementos infinitos; cosas inextensas, cosas de dimensiones infinitas), ambas rechazables. El mundo es, pues, pese a las apariencias, uno, continuo, compacto, tal como decía Parménides(ver texto ).
En la base de esta argumentación, está el hecho de que Zenón desconocía la existencia del vacío y, sobre todo, el valor finito de una suma de valores infinitamente pequeños, confundiendo así el infinito matemático con la divisibilidad material o, en todo caso, argumentaba a partir de la dificultad de explicar cómo una serie infinita de pasos o instantes pueden sumarse en una serie finita.
En otro argumento parecido, conocido con el nombre de paradoja de los granos de mijo, relatado por Simplicio, ataca la divisibilidad en lo tocante al sonido, llevando también las matemáticas pitagóricas al terreno de la física y lo material, en este caso, en el aspecto de la teoría musical: un solo grano de mijo, al caer, no hace ruido, ni lo hace tampoco una milésima parte de grano; pero sí hacen ruido al caer mil granos de trigo. ¿Es que los sonidos no pueden relacionarse entre sí como los objetos que causan los sonidos? ¿Dónde está, pues, el fundamento de la teoría musical de los pitagóricos, que relacionaban las proporciones matemáticas con las proporciones de las cuerdas en tensión?
Aquiles y la tortuga
La paradoja de Aquiles es el segundo argumento contra el movimiento. El semidiós Aquiles, el más veloz de los griegos, apuesta una carrera con uno de los más lentos animales terrestres, la tortuga. El guerrero (A) otorga magnánimo una ventaja al quelonio, que parte desde el punto T. Cuando Aquiles llegue a este punto, la tortuga, supone Zenón, habrá alcanzado otra ventaja (a), y aun cuando Aquiles llegue pronto a este punto, queda todavía otra ventaja más alcanzada por la tortuga; y así infinitamente(ver texto ). Aquiles no puede, con todos sus trabajos, alcanzar a la tortuga.
La dicotomía
Los males de Aquiles son peores de lo previsto, si se tiene en cuenta que, por la paradoja de la dicotomía, en realidad ni tan sólo puede moverse (Aristóteles, Física, VI, 9, 239b 9) o, en el mejor de los casos, no es capaz siquiera de competir consigo mismo en el estadio(ver texto ).
Para llegar, partiendo de un punto inicial (A) a otro punto determinado (C), Aquiles o cualquier cuerpo en movimiento, ha de atravesar antes el punto medio del espacio existente (B). Para llegar a esta mitad de camino, ha de pasar antes por el punto medio de dicha distancia (B; y para llegar a esta nueva mitad de camino del anterior, ha de llegar también al punto medio de esta distancia (B'; y así indefinidamente, por lo que no es posible que Aquiles, o cualquier cuerpo en movimiento, en realidad se mueva.
La flecha
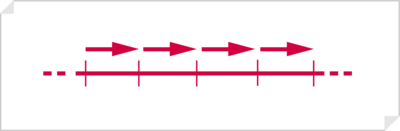
Tercera de las paradojas de Zenón que nos ha transmitido, entre otros, Aristóteles (Física VI, 9, 239b 5-7). Parte del supuesto de que un cuerpo en reposo ocupa un espacio «igual a sí mismo». Ahora bien, una flecha en movimiento ocupa también, para cada instante, un espacio igual a ella misma; por tanto, está en reposo (ver texto ).
El estadio
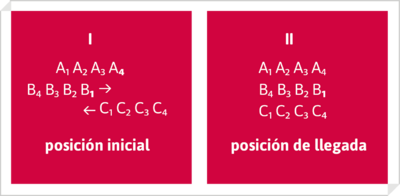
Cuarto argumento paradójicocon que Zenón, al decir de Aristóteles (Física VI, 9, 239b 33) rebate la posibilidad de movimiento.Se basa, igual que los anteriores, en el supuesto pitagórico de que el espacio y el tiempo se componen de elementos mínimos puntuales e indivisibles. Habla de dos «cuerpos sólidos» o «masas» compuestas de estos elementos puntuales, y que cruzan su movimiento en un estadio, pasando por delante de otra masa igualmente compuesta del mismo número de elementos. Partiendo de una posición inicial (I) se llega a la definitiva (II), tras el movimiento.
Los cuerposB y C tienen movimientos contrarios, pero velocidades iguales. Al pasar de la posición inicial (I) a la posición de llegada (II), han realizado un movimiento contrario, de tal manera que, para cada instante, tan puntual y mínimo como los mismos elementos componentes de las masas A, B y C, mientras el cuerpo de B pasa por delante de dos elementos de A, utilizando dos instantes, el mismo cuerpo de B pasa por delante de cuatro elementos puntuales de C, utilizando para ello cuatro instantes. De modo que los B llevan a cabo, durante el mismo lapso de tiempo, dos movimientos distintos.
La fuerza de la paradoja se apoya en suponer que el tiempo, igual que el espacio, se compone de elementos indivisibles, tal como interpretaba Zenón a los pitagóricos, para quienes «las cosas se asemejaban a los números» (ver texto ).
Todos estos argumentos no pretenden mostrar no sólo la imposibilidad del movimiento, sino la imposibilidad del movimiento y de la divisibilidad, o pluralidad. Quien sostenga una u otra cosa carece de argumentos racionales y se ve abocado a la contradicción. No es posible conciliar movimiento y pluralidad, sin contradecirse. Tales argumentos, con tales supuestos, van dirigidos contra los pitagóricos, los pluralistas y los atomistas.